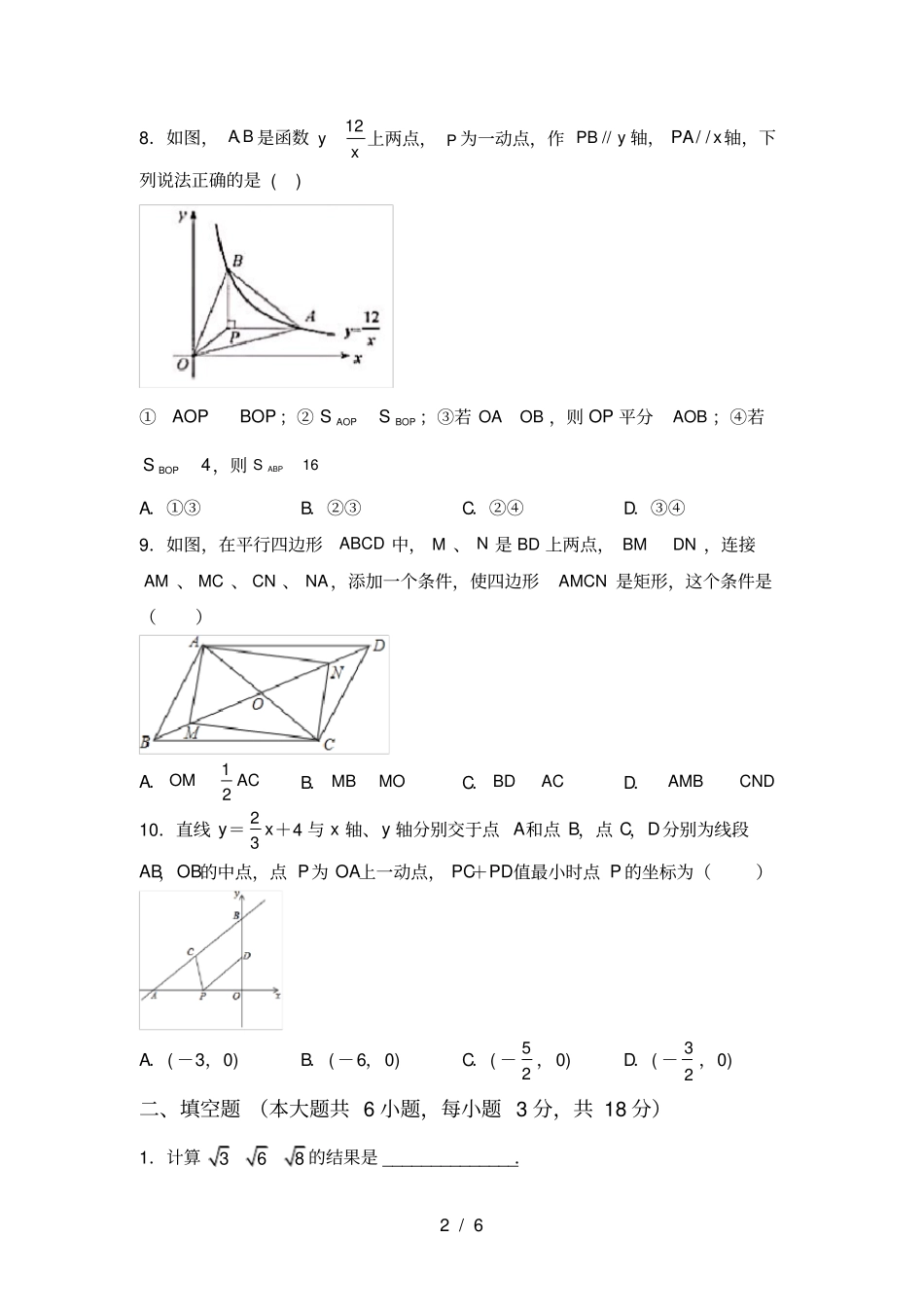
1/6人教版九年级上册数学期末考试题【及答案】班级:姓名:一、选择题(本大题共10小题,每题3分,共30分)1.﹣3的绝对值是()A.﹣3B.3C.-13D.132.不等式组111324(1)2()xxxxa有3个整数解,则a的取值范围是()A.65aB.65aC.65aD.65a3.若正多边形的一个外角是60,则该正多边形的内角和为()A.360B.540C.720D.9004.直线yxa不经过第二象限,则关于x的方程2210axx实数解的个数是().A.0个B.1个C.2个D.1个或2个5.已知关于x的一元二次方程22(1)210axxa有一个根为0x,则a的值为()A.0B.C.1D.16.对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是()A.c<﹣3B.c<﹣2C.c<14D.c<17.如图,直线AB∥CD,则下列结论正确的是()A.∠1=∠2B.∠3=∠4C.∠1+∠3=180°D.∠3+∠4=180°2/68.如图,AB、是函数12yx上两点,P为一动点,作//PBy轴,//PAx轴,下列说法正确的是()①AOPBOP;②AOPBOPSS;③若OAOB,则OP平分AOB;④若4BOPS,则16ABPSA.①③B.②③C.②④D.③④9.如图,在平行四边形ABCD中,M、N是BD上两点,BMDN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是()A.12OMACB.MBMOC.BDACD.AMBCND10.直线y=23x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为()A.(-3,0)B.(-6,0)C.(-52,0)D.(-32,0)二、填空题(本大题共6小题,每小题3分,共18分)1.计算368的结果是______________.3/62.因式分解:3222xxyxy﹣__________.3.若a、b为实数,且b=22117aaa+4,则a+b=__________.4.如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为_____________.5.如图,点A,B是反比例函数y=kx(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA,BC,已知点C(2,0),BD=2,S△BCD=3,则S△AOC=__________.6.已知抛物线20yaxbxca的对称轴是直线1x,其部分图象如图所示,下列说法中:①0abc;②0abc;③30ac;④当13x时,0y,正确的是__________(填写序号).三、解答题(本大题共6小题,共72分)1.解方程:2142242xxxx=12.先化简,再求值:24211326xxxx,其中21x.4/63.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.(1)求抛物线的解析式和直线AC的解析式;(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.4.在?ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F(1)在图1中证明CE=CF;(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.5.随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时5/6尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:请依据统计结果回答下列问题:(1)本次调查中,一共调查了位好友.(2)已知A类好友人数是D类好友人数的5倍.①请补全条形图;②扇形图中,“A”对应扇形的圆心角为度.③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?61.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.(1)求出每天的销售利润y(元)与销售单价x(元)之间...