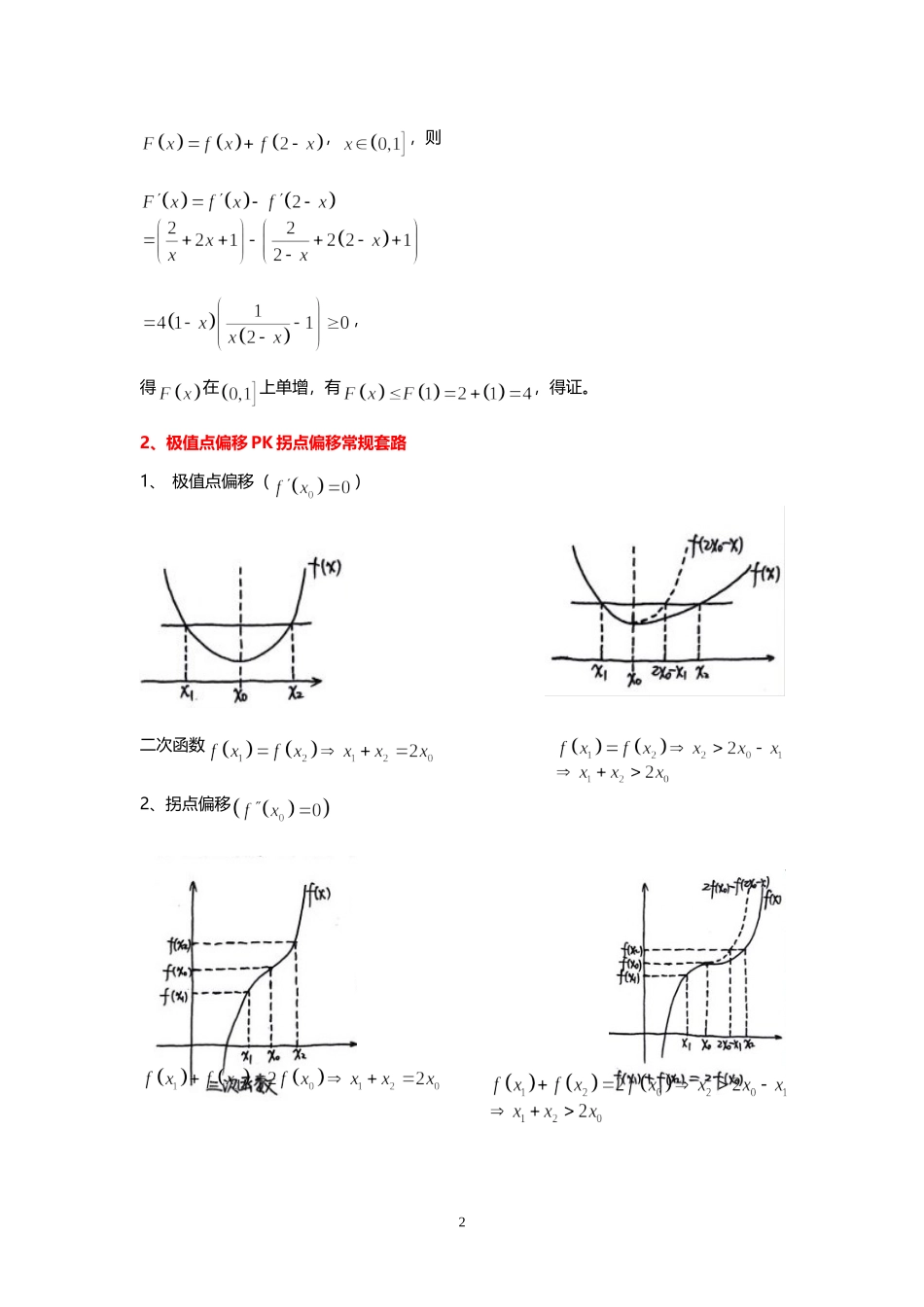
1极值点偏移问题专题(0)——偏移新花样(拐点偏移)例1已知函数,若正实数,满足,求证:。证明:注意到,,,则(1,2)是图像的拐点,若拐点(1,2)也是的对称中心,则有,证明则说明拐点发生了偏移,作图如下想到了“极值点偏移”,想到了“对称化构造”,类似地,不妨将此问题命名为“拐点偏移”,仍可用“对称化构造”来处理.不妨设,要证2,,则,得在上单增,有,得证。2、极值点偏移PK拐点偏移常规套路1、极值点偏移()二次函数2、拐点偏移3极值点偏移问题专题(1)——对称化构造(常规套路)例1(2010天津)已知函数.(1)求函数的单调区间和极值;(2)已知函数的图像与的图像关于直线对称,证明:当时,;(3)如果,且,证明:.4点评:该题的三问由易到难,层层递进,完整展现了处理极值点偏移问题的一般方法——对称化构造的全过程,直观展示如下:例1是这样一个极值点偏移问题:对于函数,已知,,证明.再次审视解题过程,发现以下三个关键点:(1),的范围;(2)不等式;(3)将代入(2)中不等式,结合的单调性获证结论.把握以上三个关键点,就可轻松解决一些极值点偏移问题.5例2(2016新课标Ⅰ卷)已知函数有两个零点.(1)求的取值范围;(2)设,是的两个零点,证明:.解:(1),过程略;(2)由(1)知在上,在上,由,可设.构造辅助函数当时,,,则,得在上,又,故,即.将代入上述不等式中得,又,,在上,故,.通过以上两例,相信读者对极值点偏移问题以及对称化构造的一般步骤有所了解.但极值点偏移问题的结论不一定总是,也可以是,借鉴前面的解题经验,我们就可给出类似的过程.例3已知函数的图像与直线交于不同的两点,,求证:.6证明:(i),得在上,在上;当时,;;当时,;当时,(洛必达法则);当时,,于是的图像如下,得.小结:用对称化构造的方法解极佳点偏移问题大致分为以下三步:step1:求导,获得的单调性,极值情况,作出的图像,由得,的取值范围(数形结合);step2:构造辅助函数(对结论,构造;对结论7,构造),求导,限定范围(或的范围),判定符号,获得不等式;step3:代入(或),利用及的单调性证明最终结论.