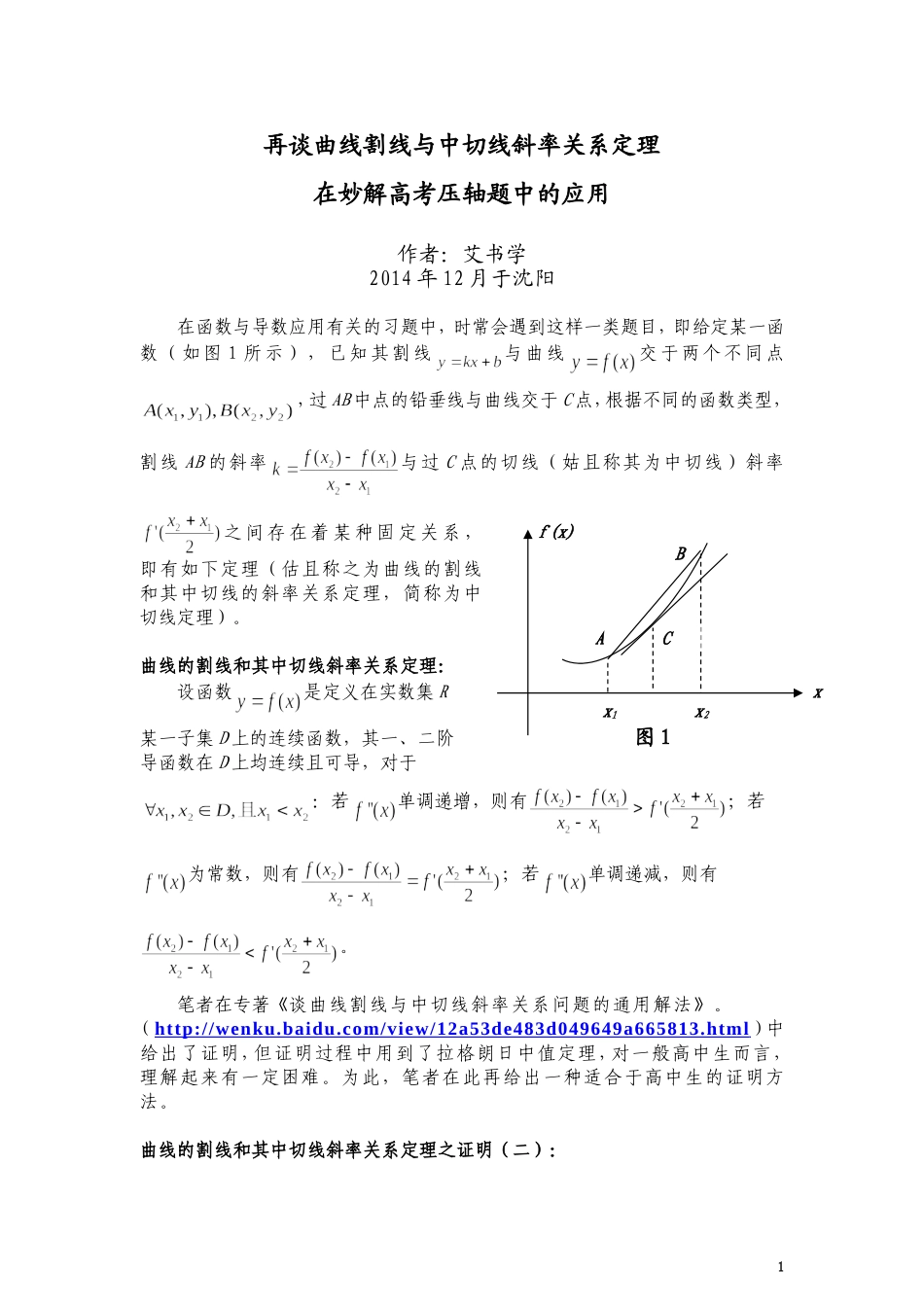
再谈曲线割线与中切线斜率关系定理在妙解高考压轴题中的应用作者:艾书学2014年12月于沈阳在函数与导数应用有关的习题中,时常会遇到这样一类题目,即给定某一函数(如图1所示),已知其割线与曲线交于两个不同点,过AB中点的铅垂线与曲线交于C点,根据不同的函数类型,割线AB的斜率与过C点的切线(姑且称其为中切线)斜率之间存在着某种固定关系,即有如下定理(估且称之为曲线的割线和其中切线的斜率关系定理,简称为中切线定理)。曲线的割线和其中切线斜率关系定理:设函数是定义在实数集R某一子集D上的连续函数,其一、二阶导函数在D上均连续且可导,对于:若单调递增,则有;若为常数,则有;若单调递减,则有。笔者在专著《谈曲线割线与中切线斜率关系问题的通用解法》。(http://wenku.baidu.com/view/12a53de483d049649a665813.html)中给出了证明,但证明过程中用到了拉格朗日中值定理,对一般高中生而言,理解起来有一定困难。为此,笔者在此再给出一种适合于高中生的证明方法。曲线的割线和其中切线斜率关系定理之证明(二):1BAxf(x)x2x1C图1设,则当即时,,故在定义域内单调递增,且在定义域内单调递减。先讨论的情形:当时,因,故,,即,进而有,所以,令,即有设,则当即或时,,在定义域内单调递减;反之,当即或时,2,在定义域内单调递增。先讨论且的情形:此时单调递增,单调递增;当时,因,故,,即,进而有,所以,令,即有令,则,由于的二阶导数存在,而3故在上满足拉格朗日中值定理成立的条件,由此知,使得,即有成立,所以设由于的二阶导数存在,而故在上满足拉格朗日中值定理成立的条件,由此知,使得,即有成立,所以若,则单调递增。而,即4即有当为常数时,上式中,显然命题中等号成立;当时,证法与的情形完全相同。本文主要通过实例使读者体会该定理在解决部分高考压轴题中的巧妙应用。【例题1】(直接应用:吉林省长春市2014届高三毕业班第二次调研测试题)已知函数.(1)求的单调区间和极值;(2)设,,且,证明:.解:(Ⅰ)易求得的单调递减区间为,单调递增区间为。(Ⅱ)由于,故,故在定义域上单调递减。由中切线定理即知,。【例题2】(直接应用:2011辽宁卷理科21题)已知函数.(I)讨论的单调性;(II)设,证明:当时,;(III)若函数的图像与轴交于A,B两点,线段AB中点的横坐标为,证明:.解:(I)易知:当时上单调增加;当时,上单调增加,在上单调减少.(II)证明略。(III)设函数的图像与轴交于,则有。由于故且5,故在定义域上单调递增。由中切线定理即知,,命题得证。【例题3】(直接应用:2005湖南卷理科21题、2010年广东省高中青年教师命题大赛参赛试题、2013年辽宁省重点中学协作体领航高考预测理科试题、2014年鄂尔多斯市高考模拟理科试题)已知(Ⅰ)当时,求的极大值点;(Ⅱ)设函数的图象与函数的图象交于、两点,过线段的中点做轴的垂线分别交、于点、,证明:在点处的切线与在点处的切线不平行.解:(I)易知当时,的极大值点为.(II)依题意设,记,则。由于故且,故在定义域上单调递增。由中切线定理知,。另一方面,由于为常数,由中切线定理知,。由于为曲线的交点,故有,,由6此知,命题得证。【例题4】(微变应用:2014届杭州市高考模拟考试样题理科22题)已知函数,(Ⅰ)已知求的单调区间;(Ⅱ)已知若,,求证:122xxt.解:(I)略。(II)依题意,由于故且,故在定义域上单调递减,单调递增。由中切线定理知,;又因为单调递减,即知命题成立。【例题5】(变式拓展:2009辽宁卷理科21题、2010年广东省高中青年教师命题大赛参赛试题)已知函数。(Ⅰ)讨论函数的单调性;(Ⅱ)证明:若,则对任意,有。解:(I)易知当时,在单调递增,在单调递减;当时,在单调递增,在单调递减.(II)依题意,由于故且,故在定义域7上单调递增。由中切线定理知,;而当时,。综上所述知,成立。【例题6】(变式拓展:2010天津卷理科21题)已知函数(Ⅰ)求函数的单调区间和极值;(Ⅱ)已知函数的图象与函数的图象关于直线对称,证明当时,;(Ⅲ)如果,且,证明。解:(Ⅰ)易知在上单调增加,在上单调...