指数函数精品课件VIP免费

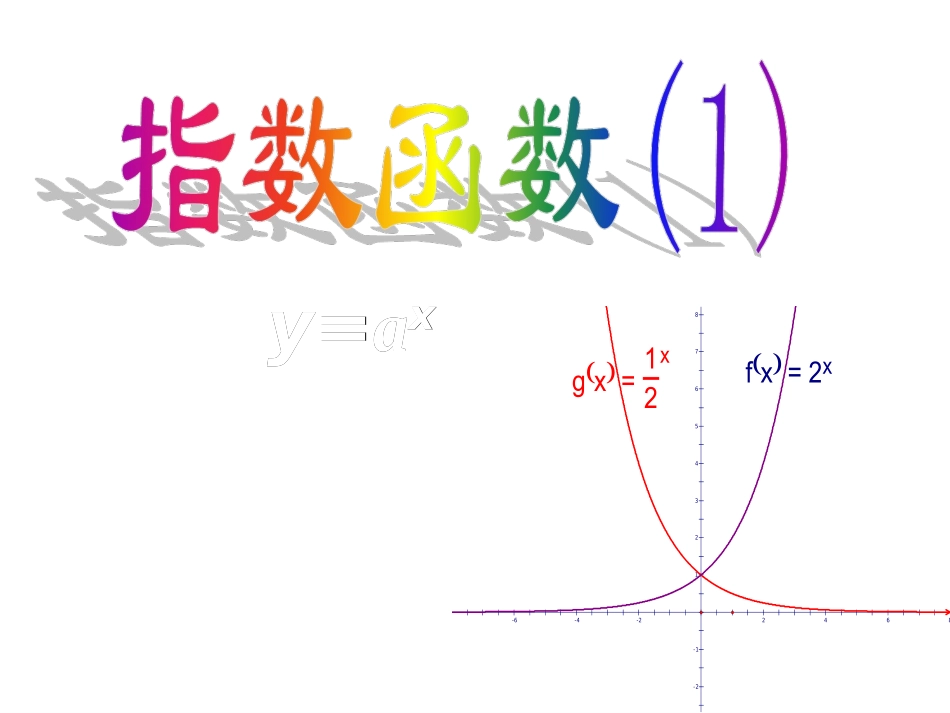
y=y=aaxx87654321-1-2-6-4-22468gx=12xfx=2x一、问题引入(1)一张白纸对折一次得两层，对折两次得4层，对折3次得8层，问若对折x次所得层数为ｙ，则y与x的函数关系是：（２）有人要走完一段路，第一次走这段路的一半，每次走余下路程的一半，请问最后能达到终点吗？如果我们引入两个变量x—次数，y—剩下路程，请问能不能建立y关于x的函数的关系？问题问题：：我们在前面学习了分数指数幂我们在前面学习了分数指数幂,,请问大家刚才两个函数能不能把定义域拓展到整个请问大家刚才两个函数能不能把定义域拓展到整个实数集实数集RR？？*2,xyxN显然可以得到这样两个函数：12,2xxyyxR*1,2xyxN指数函数的概念函数y=ax叫作指数函数自变量底数（常数）xya思考：这里的a可以取什么样的值？0a当xx0,a无意义2a当1,2x不存在1a当1,xa没有研究价值一般地，函数y=ax(a＞0且a≠1)叫做指数函数，其中x是自变量，其定义域为R。口答练习：判断下列函数是否是指数函数？口答练习：判断下列函数是否是指数函数？11））y=2y=2－－xx2)y=2)y=－－0.50.5xx33））y=3·2y=3·2xx44））y=xy=x0.60.6我们已经知道了指数函数的形式了，那么下面让我们来探究它的性质，首先从图象开始！xx……--33--22--11--0.50.5000.50.5112233…………0.130.130.250.250.50.50.710.71111.41.4224488…………8844221.41.4110.710.710.50.50.250.250.130.13……2x2x在同一坐标系中分别作出如下函数的图像：12()xy2xy与2xy3xy3xy13()xy与xx……--2.52.5--22--11--0.50.5000.50.511222.52.5…………0.060.060.10.10.30.30.60.6111.71.7339915.615.6…………15.615.699331.71.7110.60.60.30.30.10.10.060.06……3x3xx43210-1-2-3-412345678y110()xy3xy2xy10xy12()xy13()xy10xy01)y>1108642-2-55y=ax(01的图象和性质：(01)xyaaa且图图象象性性质质1.1.定义域：定义域：2.2.值域：值域：3.3.恒恒过点，即过点，即x=x=时，时，y=y=4.4.在在RR上是上是函数函数在在RR上是函数上是函数1a01axy01xy01R(0,)(0,1)01增减例1、比较下列各题中两个值的大小：①，2.51.53.21.5分析：利用指数函数单调性2.51.53.21.5，的底数是1.5，它们可以看成函数1.5xy当x=2.5和3.2时的函数值；解:因为1.5>1，所以函数1.5xy在R上是增函数，而2.5<3.2，所以，2.53.21.51.5xy01②，1.20.51.50.5解:因为0<0.5<1，所以函数0.5xy在R上是减函数，而-1.2>-1.5，所以，1.21.50.50.5xy01利用函数的单调性利用函数的单调性（3）0.31.21.5,0.8解：由指数函数的性质知0.301.51.511.200.80.81而0.31.21.50.8与特殊值“１”比较练习：一、判断大小0.340.440.340.40.30.30.10.40.1思考：求满足下列不等式的正数a的范围6235aa正数的范围.a655aa正数的范围.a(1,)(0,1)分析:应用指数函数的单调性比较大小问题的处理方法：比较大小问题的处理方法：11：看类型：看类型22：同底用单调性：同底用单调性3:3:其它类型找中间量：其它类型找中间量：a>b,b>ca>b,b>c则则a>ca>c例2（1）已知，求实数的取值范围0.533xx解：3xy在R上是增函数又0.533x0.5x即的取值范围为x[0.5,)（2）已知，求实数的取值范围x0.225x解：0.2xy在R上是减函数2221250.2,0.20.25x2x即的取值范围为x(2,)这也是含变量的大小比较——单调性的应用练习：解不等式2312()2xxx由指数函数的单调性可得：23xxx整理得：2230xx{|31}xx原不等式的解集为：解得：31x解：原不等式等价于：2322xxx小结：形如：af(x)1时原不等式等价于：f(x)＜g(x)当0