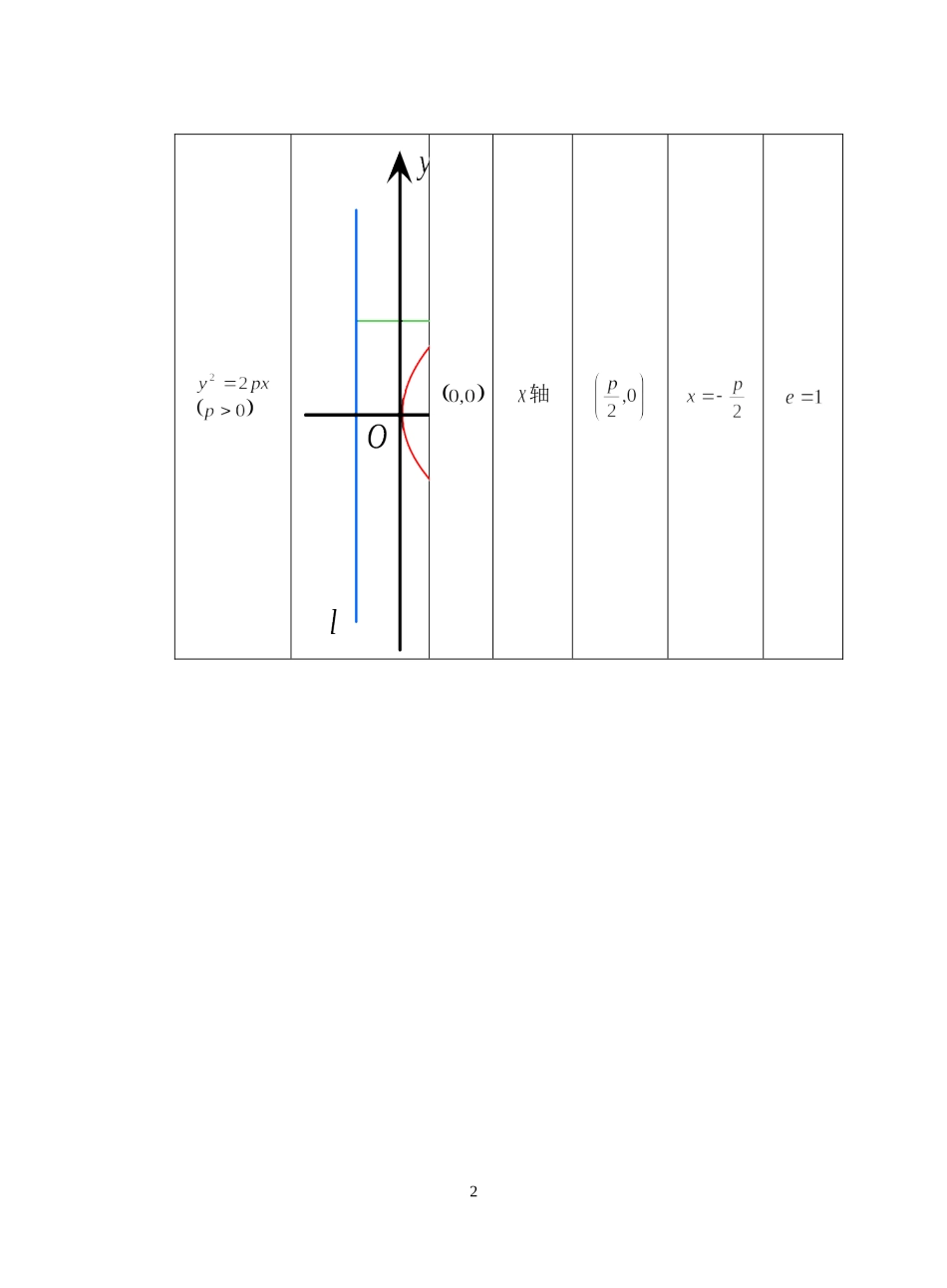
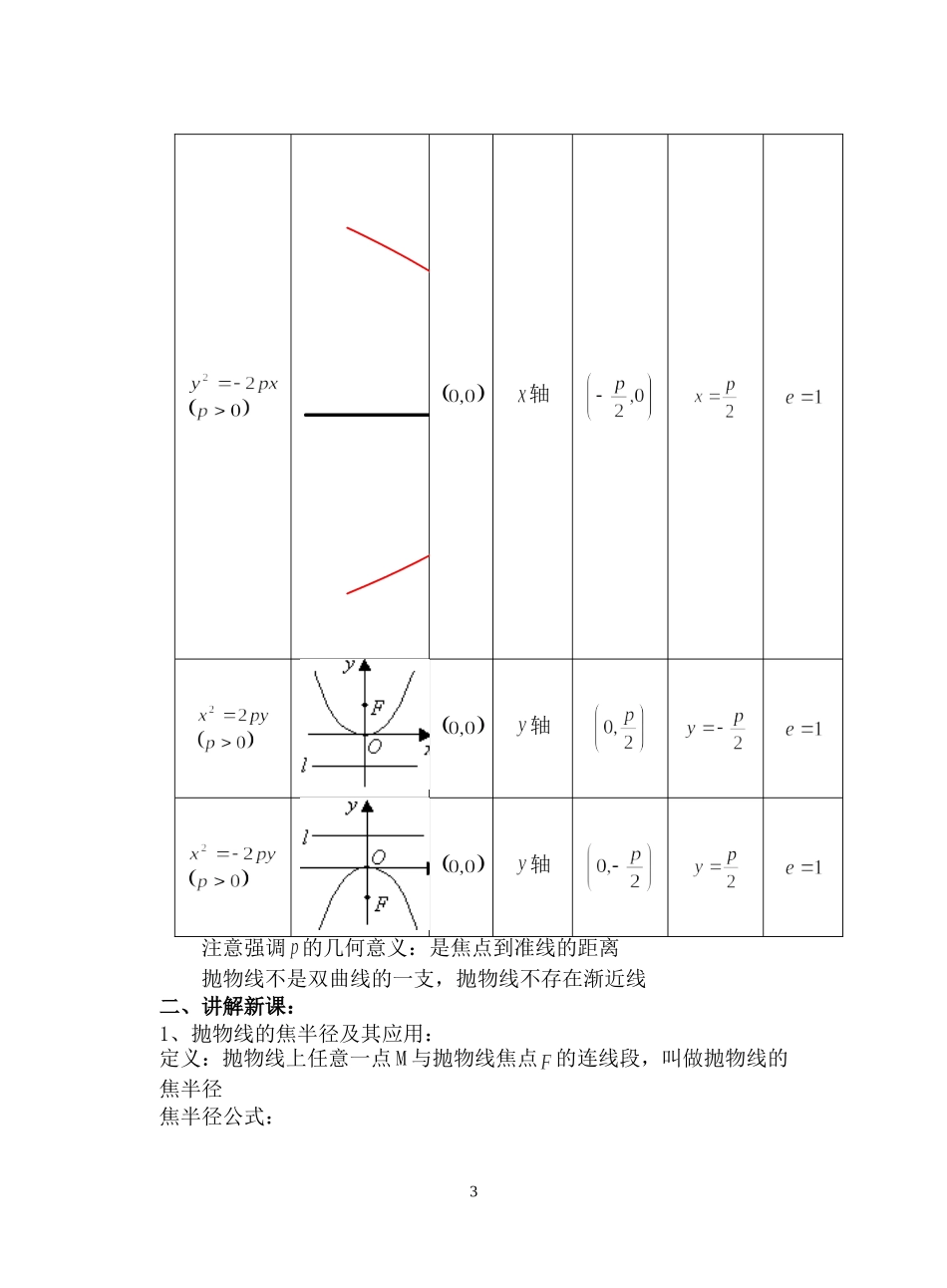
课题:8.6抛物线的简单几何性质通河一中方华教学目的:1、掌握抛物线的范围、对称性、顶点、离心率等几何性质2、掌握焦半径公式、直线与抛物线位置关系等相关概念及公式3、在对抛物线几何性质的讨论中,注意数与形的结合与转化教学重点:抛物线的几何性质及其运用教学难点:抛物线几何性质的运用授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪教学过程:一、复习引入:抛物线的几何性质:标准方程图形顶点对称轴焦点准线离心率1轴2轴轴轴注意强调的几何意义:是焦点到准线的距离抛物线不是双曲线的一支,抛物线不存在渐近线二、讲解新课:1、抛物线的焦半径及其应用:定义:抛物线上任意一点M与抛物线焦点的连线段,叫做抛物线的焦半径焦半径公式:3抛物线,抛物线,抛物线,抛物线,2、直线与抛物线:(1)位置关系:相交(两个公共点或一个公共点);相离(无公共点);相切(一个公共点)奎屯王新敞新疆下面分别就公共点的个数进行讨论:对于当直线为,即,直线平行于对称轴时,与抛物线只有唯一的4交点当,设将代入,消去y,得到关于x的二次方程奎屯王新敞新疆若,相交;,相切;,相离5奎屯综上,得:联立,得关于x的方程当(二次项系数为零),唯一一个公共点(交点)奎屯王新敞新疆6当,则若,两个公共点(交点)奎屯王新敞新疆,一个公共点(切点)奎屯王新敞新疆,无公共点(相离)7奎屯(2)相交弦长:弦长公式:,其中a和分别是中二次项系数和判别式,k为直线的斜率。当代入消元消掉的是y时,得到,此时弦长公式相应的变为:8奎屯王新敞新疆(3)焦点弦:定义:过焦点的直线割抛物线所成的相交弦。焦点弦公式:设两交点,可以通过两次焦半径公式得到:当抛物线焦点在x轴上时,焦点弦只和两焦点的横坐标有关:抛物线,9抛物线,奎屯王新敞新疆当抛物线焦点在y轴上时,焦点弦只和两焦点的纵坐标有关:抛物线,10奎屯抛物线,奎屯王新敞新疆(4)通径:定义:过焦点且垂直于对称轴的相交弦直接应用抛物线定义,得到通径:11(5)若已知过焦点的直线倾斜角则(6)常用结论:和和奎屯王新敞新疆3、抛物线的法线:过抛物线上一点可以作一条切线,过切点所作垂直于切线的直线叫做抛物线在这点的法线,抛物线的法线有一条重要性质:经过抛物线上一点作一直线平行于抛物线的轴,那么经过这一点的法线平分这条直线和这点与焦点连线的夹角如图12xy平行于轴法线切线O抛物线的这一性质在技术上有着广泛的应用.例如,在光学上,如果把光源放在抛物镜的焦点F处,射出的光线经过抛物镜的反射,变成了平行光线,汽车前灯、探照灯、手电筒就是利用这个光学性质设计的.反过来,也可以把射来的平行光线集中于焦点处,太阳灶就是利用这个原理设计的奎屯王新敞新疆4、抛物线的参数方程:(t为参数)三、讲解范例:正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线上,求这个正三角形的边长。分析:观察图,正三角形及抛物线都是轴对称图形,如果能证明x轴是它们公共的对称轴,则容易求出三角形边长。解:如图,设正三角形OAB的顶点A、B在抛物线上,且坐标分别为、,则,又|OA|=|OB|,所以即13xyBAO ,∴由此可得,即线段AB关于x轴对称因为x轴垂直于AB,且∠AOx=30°,所以所以,奎屯王新敞新疆四、课堂练习:1、正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线上,求这个正三角形的边长2、正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线上,求正三角形外接圆的方程14奎屯王新敞新疆依题意可知圆心在轴上,且过原点,故可设圆的方程为:,又 圆过点,∴所求圆的方程为3、已知的三个顶点是圆与抛物线的交点,且的垂心恰好是抛物线的焦点,求抛物线的方程。4、已知直角的直角顶点为原点,、在抛物线上,(1)分别求、两点的横坐标之积,纵坐标之积;(2)直线是否经过一个定点,若经过,求出该定点坐标,若不经过,说明理由;(3)求点在线段上的射影的轨迹方程15奎屯王新敞新疆5、已知直角的直角顶点为原点,、在抛物线上,原点在直线上的射影为,求抛物线的方程。6、已知抛物线与直线相交于、两点,以弦长为直径的圆恰好过原点,求此抛物线的方程。7、...