极坐标计算二重积分VIP免费

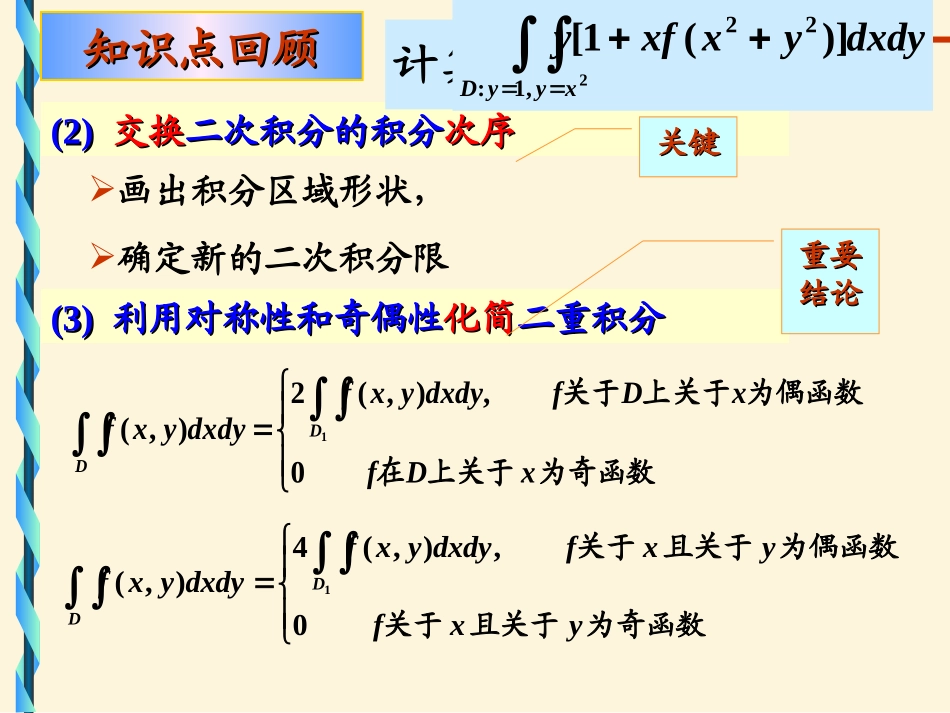
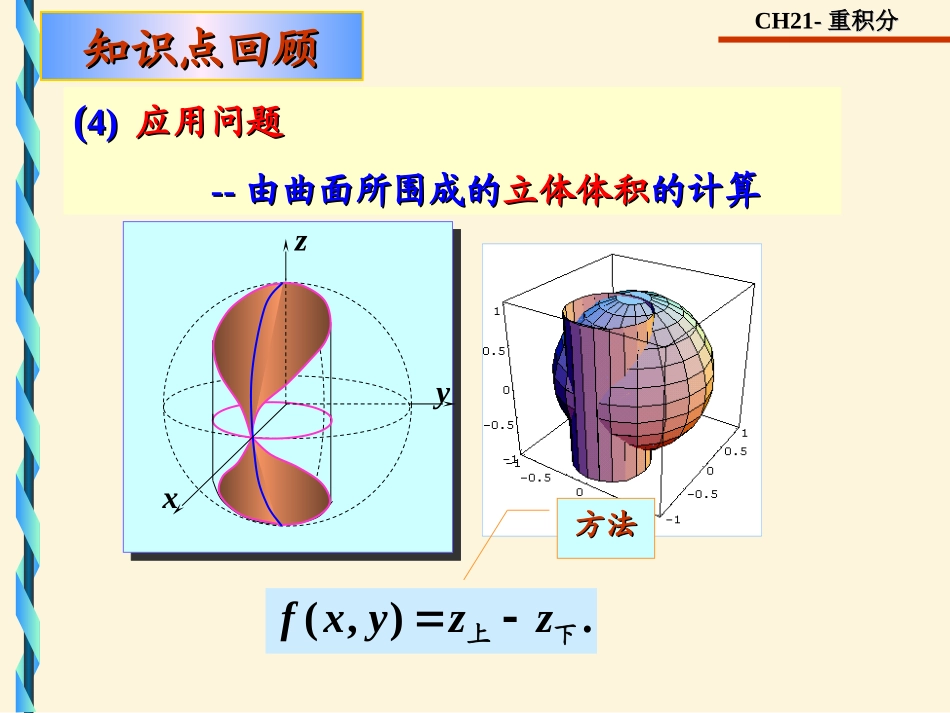
CH21--重积分重积分DDdxdyyxfdyxf),(),((1)(1)直角坐标下直角坐标下累次积分累次积分的计算公式的计算公式.),(),()()(21Dbaxxdyyxfdxdyxf.),(),()()(21Ddcyydxyxfdydyxf［［YY－－型型］］［［XX－－型型］］知识点回顾知识点回顾确定累次积分限关键关键直角坐标系下的直角坐标系下的面积元素面积元素CH21--重积分重积分(2)(2)交换交换二次积分的积分二次积分的积分次序次序知识点回顾知识点回顾画出积分区域形状，确定新的二次积分限(3)(3)利用对称性和奇偶性利用对称性和奇偶性化简化简二重积分二重积分DDxDfxDfdxdyyxfdxdyyxf为奇函数上关于在为偶函数关于上关于0,),(2),(1关键关键重要重要结论结论1002xydyedxI计算2,1:22)](1[xyyDdxdyyxxfyDDyxfyxfdxdyyxfdxdyyxf为奇函数且关于关于为偶函数且关于关于0,),(4),(1CH21--重积分重积分知识点回顾知识点回顾((4)4)应用问题应用问题----由曲面所围成的由曲面所围成的立体体积立体体积的计算的计算.),(下上zzyxf方法方法yzxCH21--重积分重积分计算二重积分DdxdyyxyxI2222)sin(,其中积分区域为}41|),{(22yxyxD.解由对称性，可只考虑第一象限部分，注意：被积函数也要有对称性.DdxdyyxyxI2222)sin(412222)sin(Ddxdyyxyx14DD1D利用极坐标系计算利用极坐标系计算思思考考题题考研—填空题考研—填空题CH21--重积分重积分第二十一章第二十一章$4$4利用极坐标计算利用极坐标计算二重积分二重积分数学分析数学分析CH21--重积分重积分利用极坐标计算二重积分利用极坐标计算二重积分---249页极坐标系下的极坐标系下的面积元素面积元素的确定的确定主要内容主要内容DDdxdyyxfdyxf),(),(二重积分转化为极坐标形式二重积分转化为极坐标形式表达式表达式极坐标系下的二重积分化为极坐标系下的二重积分化为累次积分累次积分极坐标系下二重积分的极坐标系下二重积分的--------计算方法计算方法本节重点本节重点极坐标形式累次积分如何将二重积分化为确定积分限是关键本节关键本节关键CH21--重积分重积分r),(rsincosryrx),(yxM在极坐标系下Ddyxf),(?极坐标系下的面积元素面积元素如何表示？极坐标系下的区域区域如何表示？一、极坐标系下二重积分的表达式一、极坐标系下二重积分的表达式0xy极坐标系下被积函数被积函数如何表示？CH21--重积分重积分AoDiirriirrriiiiiiiiirrr2221)(21iiiirrr)2(21iiiiirrrr2)(,iiirr利用扇形的利用扇形的面积公式面积公式i计算小扇形的面积221rsrdrddddrr（用极坐标曲线划分D）面积元素面积元素1.1.极坐标系下的极坐标系下的面积元素面积元素的确定的确定极坐标系下区域的面积.DrdrdCH21--重积分重积分sincosryrx.),(Ddxdyyxf.)sin,cos(),(DDrdrdrrfdxdyyxfrD化边界曲线化边界曲线)sin,cos(rrf化被积函数化被积函数rdrd化面积元素化面积元素应用范围：应用范围：积分区域为圆域积分区域为圆域((或一部分或一部分))，被，被积函数含的用此简便积函数含的用此简便..)(22yx2.2.二重积分转化为极坐标形式的二重积分转化为极坐标形式的表达式表达式222ryx关键关键CH21--重积分重积分确定极坐标系下先r后积分的方法DoA==,).()(21r-型：)()(21)sin,cos()sin,cos(),(rdrrrfddrrdrrfdyxfDD).(1r).(2r极坐标系下的累次积分极坐标系下区域如图所示：二、极坐标系下二重积分化累次积分二、极坐标系下二重积分化累次积分方法：方法：三线三线法法CH21--重积分重积分ADo)(1r)(2rDrdrdrrf)sin,cos(区域特征（一）如图区域特征（一）如图：：,).()(21rAoD)(2r)(1r极...