231矩阵乘法的概念VIP免费

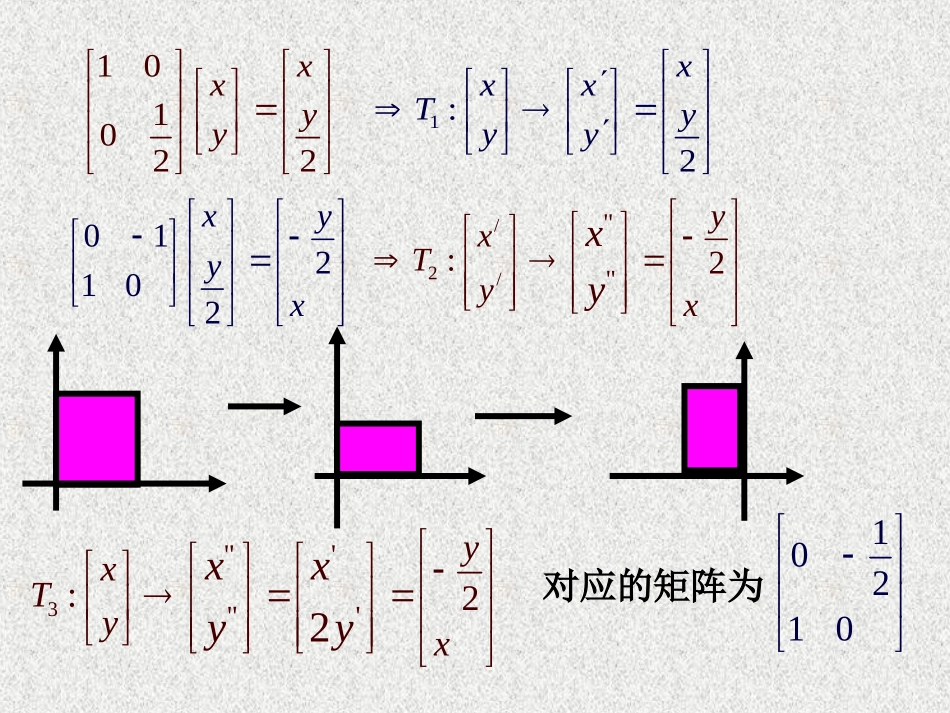
矩阵乘法的概念2001xy2:xxxTyyy二阶矩阵与平面列向量的乘法法则为:0110120111221220210220xaxayaaaayaxay2xy复习回顾101022xxyy1:2xxxTyyy012102xyyx/2/"":2yxTyxxy3"'"':22yxTyxxxyy10210对应的矩阵为规定：矩阵乘法的法则是:abefcdghaebgafbhcedgcfdh建构数学矩阵的乘法的几何意义：矩阵乘法MN的几何意义为：对向量连续实施的两次几何变换(先TN,后TM)的复合变换.建构数学当连续对向量实施n(n∈N*)次变换TM时，记作：Mn=M·M·····Mn个M112211221122112210021423100010011002例1、(1)已知A=,B=(2)已知A=,B=(3)已知A=,B=,C=计算AB，AC;,计算AB;,计算AB，BA;数学运用阅读教材37页阅读部分10312102410113201134例2、求矩阵A=与B=的乘积AB解：C=AB=10312102410113201134140(1)1101100332(1)130(1)331(1)4241(1)211120130221002301249219911数学运用BA=?AB有意义，但是BA没有意义，故要注意相乘顺序。（AB≠BA）例3、已知梯形ABCD,A(0,0),B(3,0),C(2,2),D(1,2),先将梯形作关于x轴的反射变换，再将所得图形绕原点逆时针旋转90度，求连续两次变换所对应的变换矩阵M;数学运用解：关于x轴的反射变换矩阵A=1001绕原点逆时针旋转90度的变换矩阵B=0110则M=BA=011001101001•先将梯形绕原点逆时针旋转90度，再将所得图形作关于x轴的反射变换,求连续两次变换所对应的变换矩阵M变式训练0110McossincossinA,Bsincossincos若(1)求AB，BA并对其几何意义给予解释。(2)求A2数学运用例4、(3)求Ancos2sin2sin2cos2cossinsincosnnnn在数学中，一一对应的平面几何变换都可以看做是伸压、反射、旋转、切变变换的一次或多次复合，而伸压、反射、旋转、切变等变换通常叫做初等变换，对应的矩阵叫做初等变换矩阵。本节小结•1.熟练掌握二阶矩阵与二阶矩阵的乘法.•2.理解两个二阶矩阵相乘的结果仍然是一个二阶矩阵,从几何变换角度看,它表示的原来两个矩阵对应的连续两次变换.•3.矩阵乘法MN的几何意义为对向量连续实施的两次几何变换(先TN,后TM)的复合变换.•课后思考：•根据本节内容，能得出矩阵乘法具有那些运算性质？不具有那些运算性质？课后作业完成创新课时卷