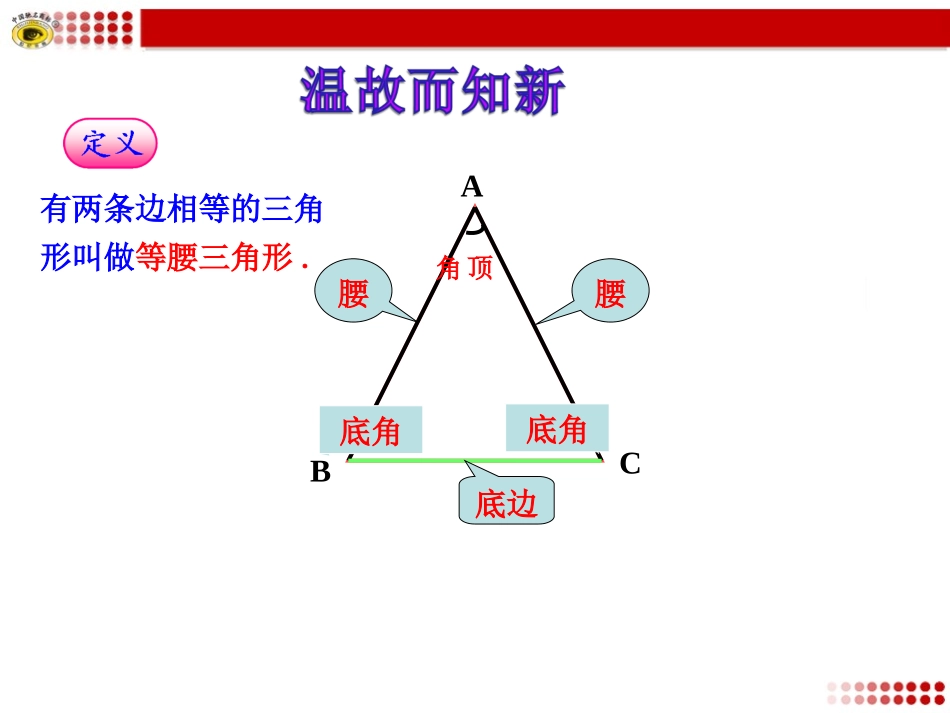
第1课时13.3等腰三角形13.3.1等腰三角形1、掌握等腰三角形的性质;2、运用等腰三角形的性质解决相关问题.有两条边相等的三角形叫做等腰三角形.ACB腰腰底边顶角底角底角ABCD如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?△ABC(AB=AC),△ADB(AD=BD)若将条件改为AB=AC,AD=BD=BC,则有多少个等腰三角形?△ABC(AB=AC)△ADB(AD=BD)△BDC(BD=BC)材料:剪刀、一张矩形纸方法:(1)先将矩形纸按图中虚线对折;(2)剪去阴影部分;(3)将剩余部分展开。大胆猜测请同学们拿出你们刚剪好的等腰三角形请同学们拿出你们刚剪好的等腰三角形纸片纸片,,它除了两腰相等以外它除了两腰相等以外,,你还能发你还能发现什么现什么??ABCD设问:你发现了什么现象,猜想等腰△ABC有哪些性质?角:B=C①∠∠②∠BAD=∠CDA③∠ADC=∠ADB=900边:④BD=CD→两个底角相等→AD为顶角∠BAC的平分线→AD为底边BC上的高→AD为底边BC上的中线结论:等腰三角形是轴对称图形;等腰三角形性质性质1等腰三角形的两个底角相等(简写成“等边对等角”);性质2等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)已知:△ABC中,AB=AC.求证:∠B=C.分析:1.如何证明两个角相等?2.如何构造两个全等的三角形?ABCABCD【证明】作△ABC的高线AD,(HL),则有∠ADB=∠ADC=90°,在Rt△ABD和Rt△ACD中AB=AC,AD=AD,∴Rt△ABD≌Rt△ACD∴∠B=∠C(全等三角形对应角相等).想一想:还有其他的方法吗?还可以作BC边上的中线或∠BAC的角平分线来解决.ABCD等腰三角形顶角的角平分线,底边上的高线,底边上的中线有什么关系?刚才的证明除了能得到∠B=∠C,你还能发现什么?(等腰三角形三线合一)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.等腰三角形的性质等腰三角形的性质1等腰三角形的两个底角相等(等边对等角)2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)例1在三角形ABC中,已知AB=AC,且∠B=80°,则∠C=__度,∠A=____度?∵AB=AC(已知)∴∠B=C∠(等边对等角)∵∠B=80°(已知)∴∠C=80°又∵∠A+B+C=180°∠∠(三角形内角和为180°)∴∠A=180°-∠B-∠C∠A=20°BCA8020等腰三角形的性质等腰三角形的性质1等腰三角形的两个底角相等(等边对等角)2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)操练操练11在三角形ABC中,已知AB=AC,且∠A=50°,则∠B=度,∠C=度?CBA∵AB=AC(已知)∴∠B=C∠(等边对等角)又∵∠A+B+C=180°∠∠(三角形内角和为180°)∠A=50°(已知)∴∠B=C=65°∠6565如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.ABCD【解】∵AB=AC,BD=BC=AD,∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2x,从而∠ABC=∠C=∠BDC=2x,于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,解得x=36°,所以,在△ABC中,∠A=36°,∠ABC=∠C=72°.【例题】xx2x2x2x随堂练习1.判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。()(2)有一个角是60°的等腰三角形,其它两个内角也为60°.()(3)等腰三角形的底角都是锐角.()(4)钝角三角形不可能是等腰三角形.()××当堂测试⒈等腰三角形一个底角为70°,它的顶角为______.⒉等腰三角形一个角为70°,它的另外两个角为__________________.⒊等腰三角形一个角为110°,它的另外两个角为_______.①顶角+2×底角=180°②顶角=180°-2×底角③底角=(180°-顶角)÷2④0°<顶角<180°⑤0°<底角<90°结论:在等腰三角形中,40°35°,35°70°,40°或55°,55°小结归纳通过本节课的学习,你有哪些收获?性质1:等边对等角性质2:“三线合一”常用来证明两角相等,求等腰三角形各角的度数.研究等腰三角形的有关问题时“三线”是常用的辅助线.等腰三角形分类讨论思想的应用作业:必做题:课本第82页3、4、7题选做题:预习课本第77---78页内容。