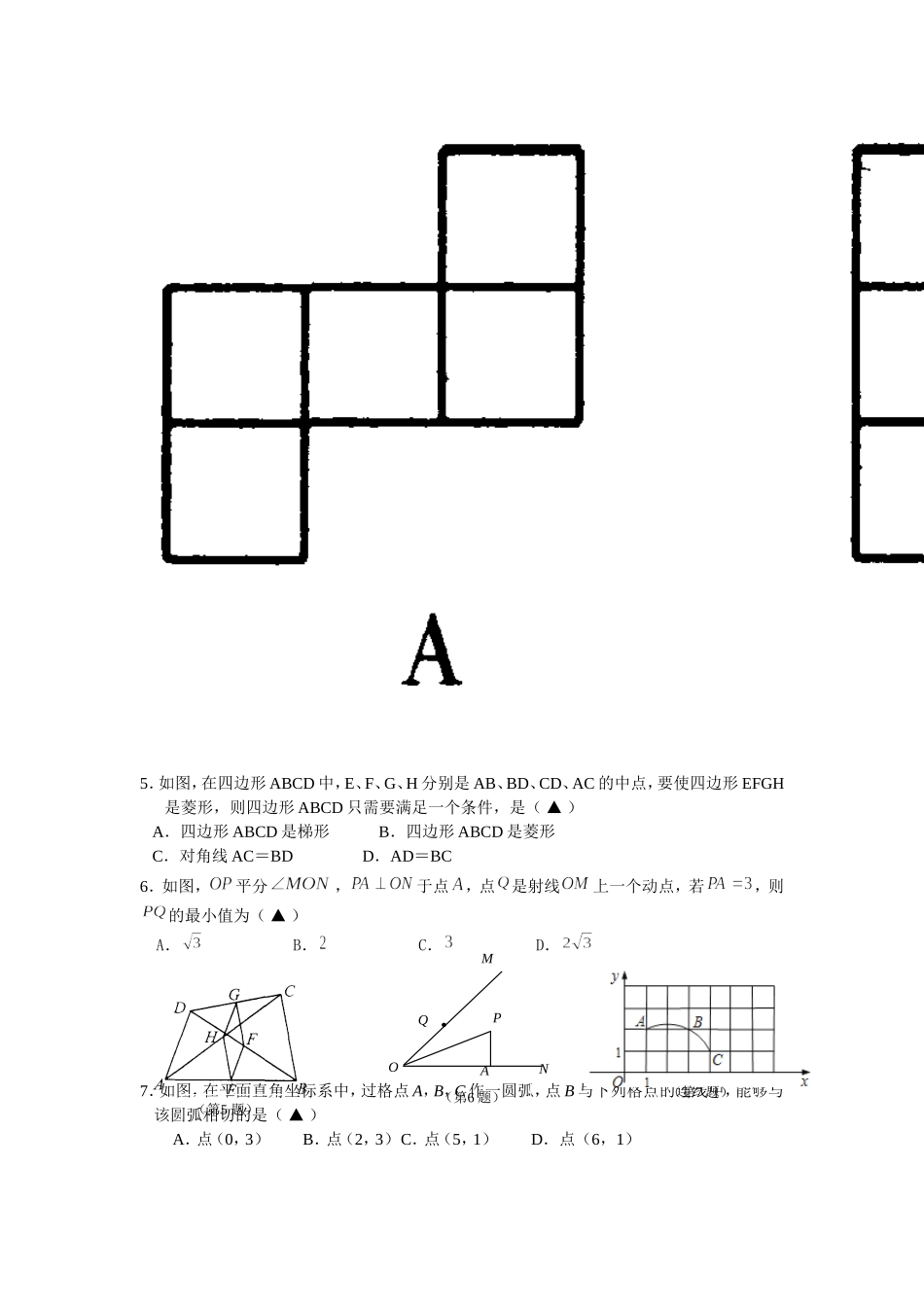
(满分:150分考试时间:120分钟)第Ⅰ卷(选择题共24分)一、选择题(本大题共8题,每题3分,共24分,每题的四个选项中,只有一个选项符合要求.)1.计算的结果是(▲)A.B.C.D.2.2014年4月份,仪征市某周的日最高气温统计如下表:则这七天中日最高气温的众数和中位数分别是(▲)A.4;4B.5;4C.4;3D.4;4.53.一次函数的图象不经过(▲)A.第一象限B.第二象限C.第三象限D.第四象限4.左图是由八个相同小正方体组合而成的几何体,则其俯视图是(▲)日期21222324252627最高气温(℃)24534675.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是(▲)A.四边形ABCD是梯形B.四边形ABCD是菱形C.对角线AC=BDD.AD=BC6.如图,平分,于点,点是射线上一个动点,若,则的最小值为(▲)A.B.C.D.7.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是(▲)A.点(0,3)B.点(2,3)C.点(5,1)D.点(6,1)APMNQO(第6题)(第5题)(第7题)8.抛物线上部分点的横坐标,纵坐标的对应值如下表:…………从上表可知,下列说法中正确的有(▲).①抛物线与轴的一个交点为;②函数的最值为;③抛物线的对称轴是;④在对称轴左侧,随的增大而增大.A.①④B.②③C.①③④D.③④第Ⅱ卷(非选择题共126分)二、填空题(本大题共10题,每题3分,共30分.把答案填在题中的横线上.)9.函数中自变量x的取值范围是▲.10.因式分解:▲.11.如图,AB、CD是水平放置的轮盘(俯视图)上两条互相垂直的直径,一个小钢球在轮盘上自由滚动,该小钢球最终停在阴影区域的概率为▲.12.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是▲.13.如图,在△ABC中,DE∥BC,,DE=4,则BC的长是▲.14.如图,一个扇形铁皮.已知,,小明将、合拢制成了一个圆锥形烟囱帽(接缝忽略不计),则烟囱帽的底面圆的半径为▲.(第11题)(第13题)EDCBAABDOC(第12题)15.如图,在平面直角坐标系中,点B的坐标是(1,0),若点A的坐标为(a,b),将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标是▲.16.将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,边AB、AC分别交半圆于点E、F,点B、E、F对应的读数分别为160°、70°、50°,则∠A的度数为▲.17.已知直角梯形ABCO的底边AO在轴上,BC//AO,AB⊥AO,对角线AC、BO相交于点D,双曲线经过点D,若AO=2BC,△BCD的面积为3,则的值为▲.18.已知:直线(为正整数)与两坐标轴围成的三角形面积为,则▲.三、解答题(本题共10个小题,共96分,解答时应写出文字说明、证明过程或演算步骤.)19.(本题满分8分)计算:.20.(本题满分8分)先化简,再求值:,其中,a是方程x2+3x+1=0的根.21.(本题满分8分)班主任老师让同学们为班会活动设计一个抽奖方案,拟使中奖概率为60%.(1)小明的设计方案:在一个不透明的盒子中,放入10个球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球则表示中奖,否则不中奖.如果小明的设计符合老师要求,则盒子中黄球应有▲个,白球应有▲个;(2)小兵的设计方案:在一个不透明的盒子中,放入4个黄球和1个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球则表示中奖,否则不中奖.该设计方案是否符合老师的要求?试说明理由.(第17题图)22.(本题满分8分)某学校为了进一步丰富学生的体育活动,欲增购一些体育器材,为此对该校一部分学生进行了一次“你最喜欢的体育活动”的问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):23.(本题满分10分)校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°....