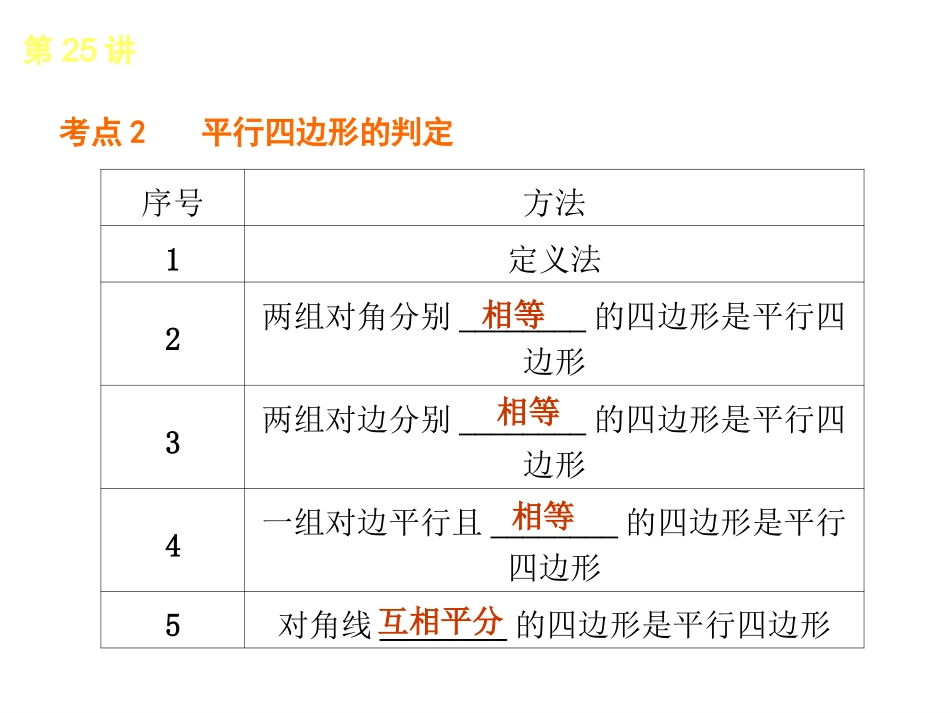
第25讲┃平行四边形考点1平行四边形的定义与性质第25讲┃考点聚焦定义两组对边分别平行的四边形是平行四边形性质(1)平行四边形的两组对边分别________;(2)平行四边形的两组对边分别________;(3)平行四边形的两组对角分别________;(4)平行四边形的对角线互相________;(5)平行四边形是中心对称图形,它的对称中心是两条对角线的交点总结若一条直线过平行四边形的对角线的交点,那么这条直线被一组对边截下的线段以对角线的交点为对称中心,且这条直线等分平行四边形的面积平行相等相等平分考点聚焦考点2平行四边形的判定第25讲┃考点聚焦序号方法1定义法2两组对角分别________的四边形是平行四边形3两组对边分别________的四边形是平行四边形4一组对边平行且________的四边形是平行四边形5对角线________的四边形是平行四边形相等相等相等互相平分考点3平行四边形的面积第25讲┃考点聚焦平行四边形的面积平行四边形的面积=底×高拓展同底(等底)等高(同高)的平行四边形面积相等两条平行线间距离在两条平行线中一条直线上任意一点到另一条直线上的距离叫做两条平行线间的距离推论夹在两条平行线间的平行线段________相等►类型之二平行四边形的性质命题角度:1.平行四边形对边的特点;2.平行四边形对角的特点;3.平行四边形对角线的特点.第25讲┃归类示例例1[2012·淮安]已知:如图25-1,在▱ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F.求证:△BEF≌△CDF.图25-1归类示例第25讲┃归类示例[解析]先由平行四边形性质,得出CD=AB=BE,AB∥CD.再由平行线的性质得∠EBF=∠DCB,结合对顶角性质,即可推出△BEF≌△CDF.第25讲┃归类示例平行四边形的性质的应用,主要是利用平行四边形的边与边,角与角及对角线之间的特殊关系进行证明或计算.第25讲┃归类示例►类型之二平行四边形的判定例2[2012·泰州]如图25-2,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.[解析]由垂直得到∠EAD=∠BCF=90°,根据AAS可证明RtAEDRtCFB△≌△,得到AD=BC,根据平行四边形的判定即可证明.第25讲┃归类示例命题角度:1.从对边判定四边形是平行四边形;2.从对角判定四边形是平行四边形;3.从对角线判定四边形是平行四边形.图25-2第25讲┃归类示例证明:∵AD∥BC,∴∠ADB=∠CBD,∵AE⊥AD,CF⊥BC,∴∠EAD=∠FCB=90°.∵AE=CF,∴△EAD≌△FCB(AAS),∴AD=CB.∵AD∥BC,∴四边形ABCD是平行四边形.第25讲┃归类示例判别一个四边形是不是平行四边形,要根据具体条件灵活选择判别方法.凡是可以用平行四边形知识证明的问题,不要再回到用三角形全等证明,应直接运用平行四边形的性质和判定去解决问题.