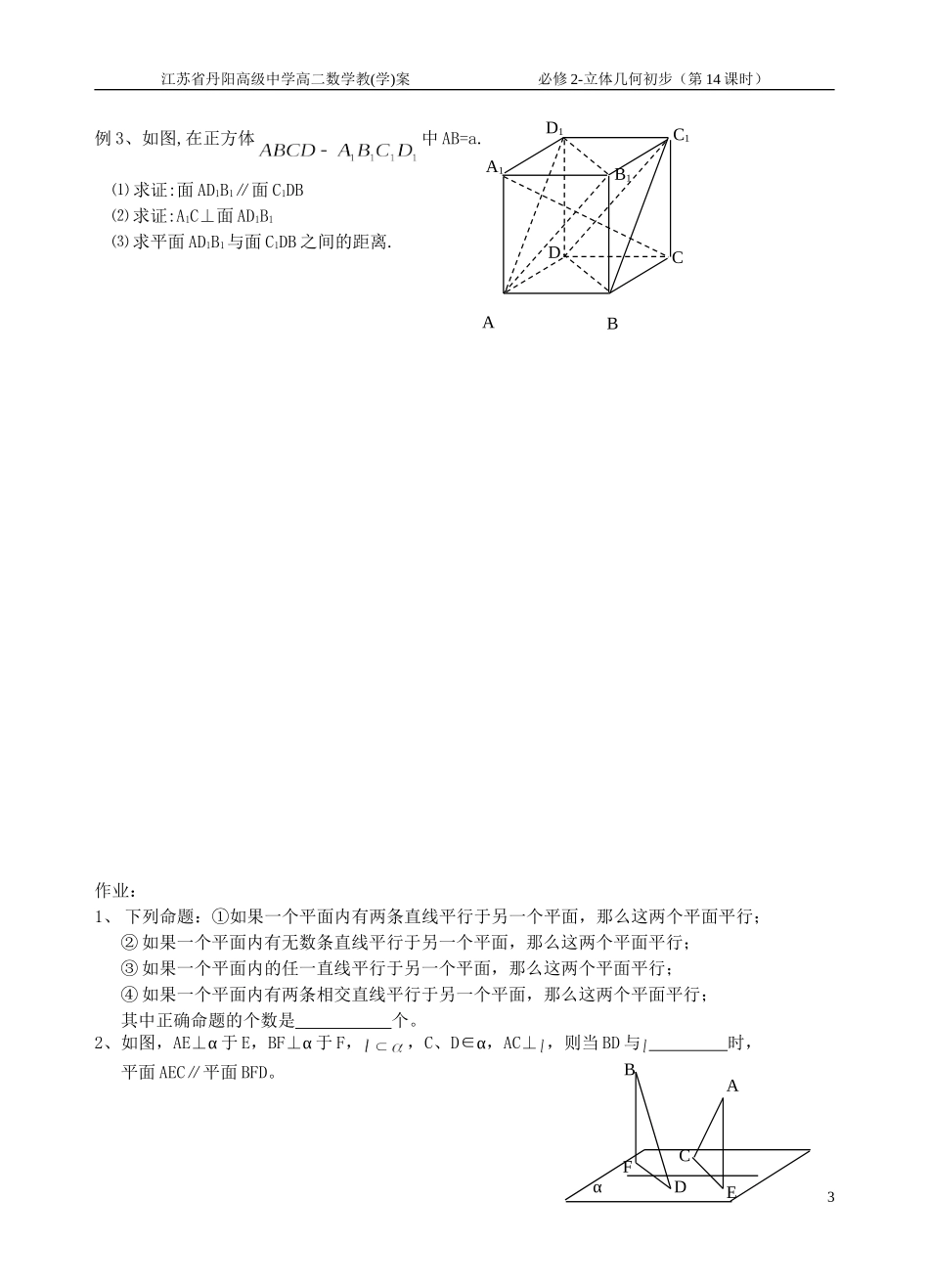
江苏省丹阳高级中学高二数学教(学)案必修2-立体几何初步(第14课时)1.2.4两个平面平行的判定与性质习题课【教学目标】:1、掌握两平行平面间距离的概念。2、综合运用面面平行的判定定理与性质定理解题【教学过程】:一、知识梳理1、两个平面平行的判定和性质:(1)定义:两个平面没有公共点,这两个平面互相平行。(2)判定定理:①如果一个平面内有两条直线都平行于另一个平面,那么这两个平面平行。②垂直于直线的两个平面平行。(3)唯一性定理:经过平面外一点有且只有一个平面和已知平面平行。(4)性质:①②③④夹在两个平行平面间的平行线段相等2、两个平行平面的距离两个平行平面的公垂线:和两个平行平面同时垂直的直线两个平行平面的公垂线段:公垂线夹在两个平行平面间的部分两个平行平面的公垂线段都相等,把公垂线段的长度叫做两个平行平面的距离。二、基础训练1、以下七个命题:(1)垂直于同一条直线的两个平面平行;(2)平行于同一条直线的两个平面平行;(3)平行于同一平面的两个平面平行;(4)一个平面内的两相交直线与另一个平面内的两条相交直线平行,则这两个平面平行;(5)与同一条直线成等角的两个平面平行;(6)一个平面上不共线的三点到另一平面的距离相等,则这两个平面平行;(7)两个平面分别与第三个平面相交所得的两条交线平行,则这两个平面平行.其中正确命题的序号是________________.2、如果在两个平面内分别有一条直线,这两条直线互相平行,那么这两个平面的位置关系一定是。3、平面,射影长分别为5㎝和9㎝,则平面之间的距离为________________.4、已知m、n是不同的直线,α、β是不重合的平面,给出下列命题:①若m∥α,则m平行于平面α内的任意一条直线;②若α∥β,mα,nβ,则m∥n;③若m⊥α,n⊥β,m∥n,则α∥β;④若α∥β,mα,则m∥β。真命题的序号是。三、典型例题1江苏省丹阳高级中学高二数学教(学)案必修2-立体几何初步(第14课时)例1、已知:∥,,点分别为线段上的点,且,求证:∥例2、如图,直线分别交两平行平面两点,直线分别交平面两点,直线分别交两平行平面两点,若求.2FpCDABQEαβ江苏省丹阳高级中学高二数学教(学)案必修2-立体几何初步(第14课时)例3、如图,在正方体中AB=a.⑴求证:面AD1B1∥面C1DB⑵求证:A1C⊥面AD1B1⑶求平面AD1B1与面C1DB之间的距离.作业:1、下列命题:①如果一个平面内有两条直线平行于另一个平面,那么这两个平面平行;②如果一个平面内有无数条直线平行于另一个平面,那么这两个平面平行;③如果一个平面内的任一直线平行于另一个平面,那么这两个平面平行;④如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行;其中正确命题的个数是个。2、如图,AE⊥α于E,BF⊥α于F,,C、D∈α,AC⊥,则当BD与时,平面AEC∥平面BFD。3αABCEFDCDA1B1C1D1AB江苏省丹阳高级中学高二数学教(学)案必修2-立体几何初步(第14课时)3、如图,直线AC、DF被三个平行平面α、β、γ所截,若AC与γ成30°角,AB=4,BC=12,DF=10,则平面β、γ间的距离为,DE=。4、若是异面直线,求证:.5、如图,棱长为a的正方体中,M、N、H分别是B1C1、C1D1、BC的中点。(1)求证:平面CMN∥平面HB1D1;(2)若平面HB1D1∩CD=G,求证:G为CD中点。6、是所在平面外一点,分别是的重心.(1)求证:平面;(2)求.4αβγABCDEFABCDHMNA1B1C1D1