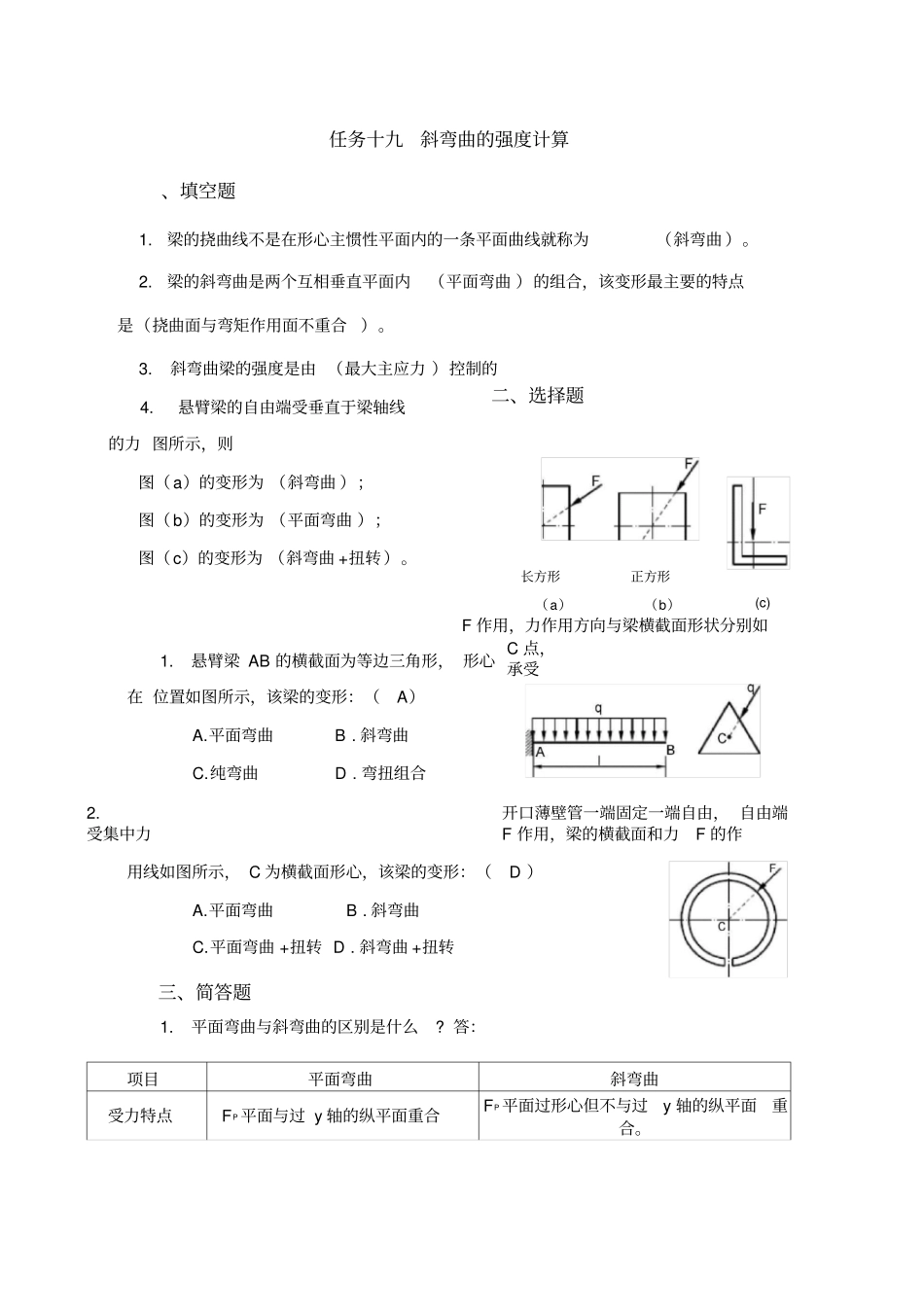
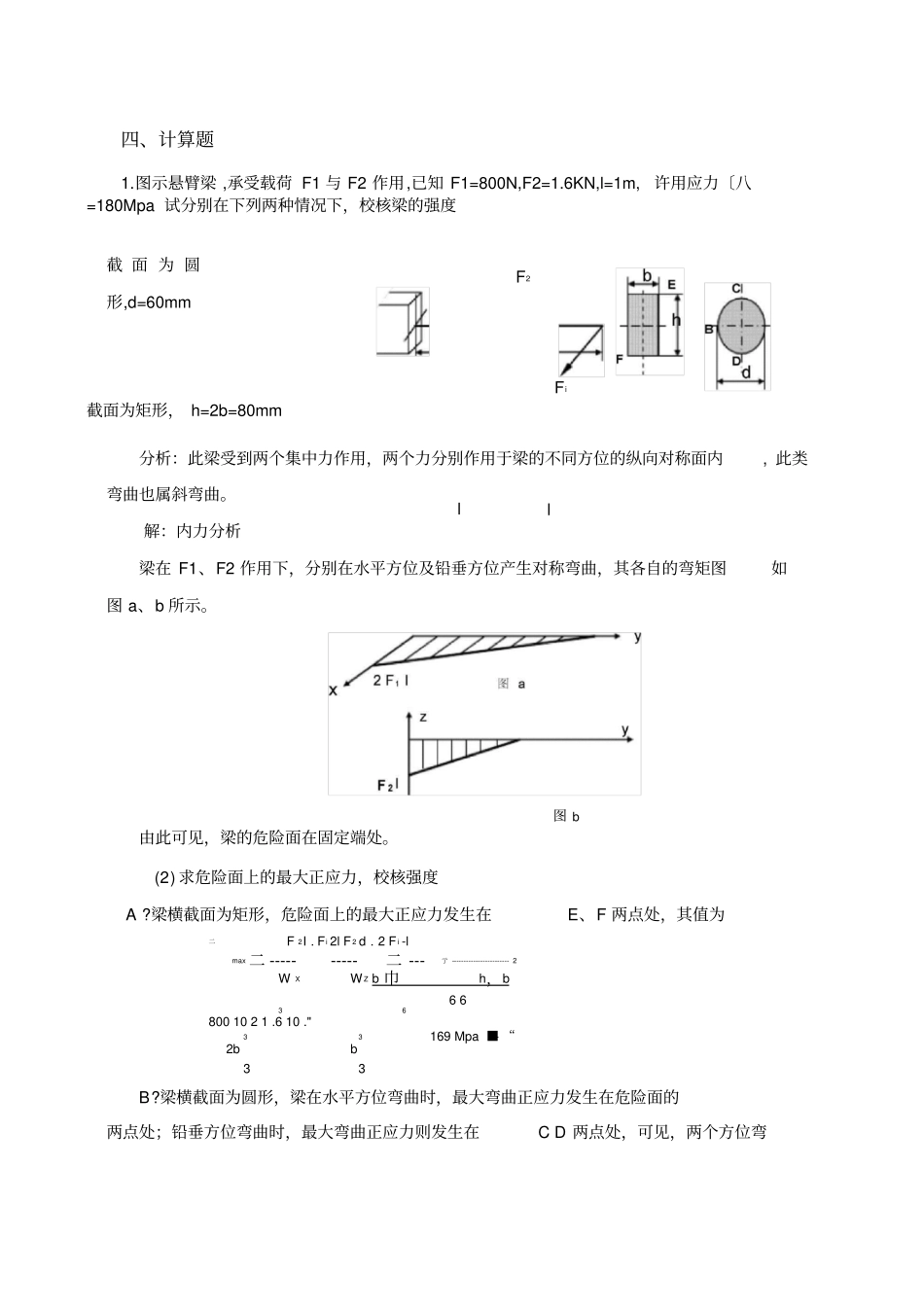
C点,承受任务十九斜弯曲的强度计算、填空题1.梁的挠曲线不是在形心主惯性平面内的一条平面曲线就称为(斜弯曲)。2.梁的斜弯曲是两个互相垂直平面内(平面弯曲)的组合,该变形最主要的特点是(挠曲面与弯矩作用面不重合)。3.斜弯曲梁的强度是由(最大主应力)控制的4.悬臂梁的自由端受垂直于梁轴线的力图所示,则图(a)的变形为(斜弯曲);图(b)的变形为(平面弯曲);图(c)的变形为(斜弯曲+扭转)。二、选择题F作用,力作用方向与梁横截面形状分别如1.悬臂梁AB的横截面为等边三角形,形心在位置如图所示,该梁的变形:(A)A.平面弯曲B.斜弯曲C.纯弯曲D.弯扭组合2.开口薄壁管一端固定一端自由,自由端受集中力F作用,梁的横截面和力F的作用线如图所示,C为横截面形心,该梁的变形:(D)A.平面弯曲B.斜弯曲C.平面弯曲+扭转D.斜弯曲+扭转三、简答题1.平面弯曲与斜弯曲的区别是什么?答:项目平面弯曲斜弯曲受力特点FP平面与过y轴的纵平面重合FP平面过形心但不与过y轴的纵平面重合。长方形正方形(a)(b)(c)中性轴特点中性轴与FP平面垂直中性轴与FP平面不垂直变形特点挠曲平面与中性轴垂直,且在FP平面内。挠曲平面与中性轴垂直,但偏离FP平面内。截面为圆形,d=60mmF2Fi四、计算题1.图示悬臂梁,承受载荷F1与F2作用,已知F1=800N,F2=1.6KN,l=1m,许用应力〔八=180Mpa试分别在下列两种情况下,校核梁的强度截面为矩形,h=2b=80mm分析:此梁受到两个集中力作用,两个力分别作用于梁的不同方位的纵向对称面内,此类弯曲也属斜弯曲。解:内力分析梁在F1、F2作用下,分别在水平方位及铅垂方位产生对称弯曲,其各自的弯矩图如图a、b所示。由此可见,梁的危险面在固定端处。(2)求危险面上的最大正应力,校核强度A?梁横截面为矩形,危险面上的最大正应力发生在E、F两点处,其值为二F2I.Fi2lF2d.2Fi-lmax二----------二---亍------------------------2WXWZb巾h,b66368001021.610."33169Mpa■-“2bb33B?梁横截面为圆形,梁在水平方位弯曲时,最大弯曲正应力发生在危险面的两点处;铅垂方位弯曲时,最大弯曲正应力则发生在CD两点处,可见,两个方位弯ll图b■maxMmaxMX2MZ2w一W二d332J(800皿2+(2""10叮=155.6MPa373.58710“94.5(mm)可取h=200mmb=120mm2)3EI7=11.6mm计算自由端的挠度。分别计算fy与fz,如图9-15(c)所示,则1.2561032331.01041060.20.12312f=fz2fy2=?.(3.72)2(11.6)2=12.18mmfy3EIz6EIz331330.336102-2.5101(32-1)131.01041060.120.2*312=3.72mm(1)zmaxymax=F1l=0.53kNm=1.5kNm13二F20.8kN2m=1.2kNm计算梁的最大拉应力及所在位置。应力的计算3?矩形截面悬臂梁如图所示,已知F1=0.5kN,F2=0.8kN,b=100mmh=150mm试Mzmax(Tmax=Wz+MymaxWy6Mzmaxbh26Mymaxhb2厂66氏1.5^102(100X150根据实际变形情况,内力的计算4.图示跨度为4m的简支梁,拟用工字钢制成,跨中作用集中力F=7kN其与横截面铅垂对称轴的夹角少=20°(图b),已知[c]=160MPa,试选择工字钢的型号(提示:先假定WWy的比值,试选后再进行校核。)解...