23【数学】第二章《平面向量》单元复习(1)课件(新人教A版必修4)VIP免费

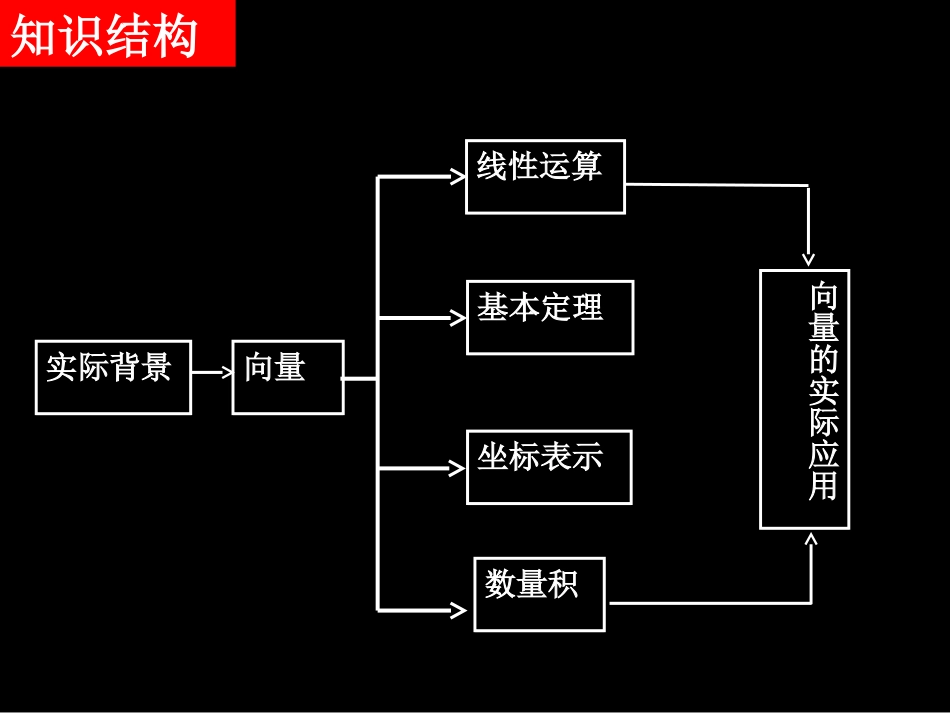
第二章平面向量单元复习第一课时知识结构实际背景基本定理坐标表示数量积向量线性运算向量的实际应用知识梳理1.向量的有关概念（1）向量：既有大小，又有方向的量.(2)向量的表示方法:几何表示:AB,a；坐标表示:a=xi+yj=(x,y)．→知识梳理1.向量的有关概念（3）向量的模（或长度）：表示向量的有向线段的长度，记作|a|.a1.设aa=(x,y),则22yxABa221221yyxx知识梳理1.向量的有关概念模为零的向量.a=0|a|=0；（3）向量的模（或长度）：（4）零向量：表示向量的有向线段的长度，记作|a|.（5）单位向量：模为1的向量.|e|=1（6）相等向量：长度相等且方向相同的向量.x1i+y1j=x2i+y2jx1=x2,且y1=y2.（7）相反向量：长度相等且方向相反的向量.（8）平行向量（共线向量）：1)方向相同或相反的非零向量.记作a//b.因为向量可以进行任意平移，平行向量总可以平移到同一直线上，故又称共线向量.2)向量平行的充要条件:a//ba=λbx1y2-x2y1=0.3)向量垂直的充要条件:aba•b=0x1x2+y1y2=0.三角形法则:2.向量的几何运算（1）加法运算：平行四边形法则:ｂa＋baaｂa＋b坐标表示:a+b=(x1+x2，y1+y2)．重要结论:AB+BC=AC．→→→（2）减法运算：三角形法则:平行四边形法则:ｂa-baa-b-ｂｂa坐标表示:a-b=(x1-x2，y1-y2)．重要结论:a–b=a+(–b)，AB=–BA，PB–PC=CB．→→→→→（3）数乘运算：λa．1)λ＞0时与a同向;λ＜0时与a反向;λ=0时,λa=0．坐标表示:λa=(λx，λy)．运算律：λ(μa)=(λμ)a;(λ+μ)a=λa+μa;λ(a+b)=λa+λb.（3）数乘运算：aλ>1时λaλ=1时λa0<λ<1时λaλ<-1时λaλ=-1时λa-1<λ<0时λaλ=0时a=0规定:2)|λa|=|λ||a|;λ其实质就是向量的伸长或缩短！（4）向量的数量积：a•b=|a||b|cosθ=x1x2+y1y2．规定：零向量与任一向量的数量积为0（4）向量的数量积：AabθBB1OBAθbB1aOθBb(B1)AaO几何意义：数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积。3.向量定理（1）共线定理：（2）基本定理：向量a（a≠0）与b共线，当且仅当有唯一一个实数λ，使b=λa.若e1、e2是同一平面内的两个不共线向量，则对于这一平面内的任意向量a，有且只有一对实数λ1，λ2，使a＝λ1e1＋λ2e2.范例分析例1在△ABC中，设a，b，已知，，试以a、b为基底表示向量.AB=uuurAC=uuur14CNCA=uuruuur34CMCB=uuuruuurMNuuuurMCBAN1324MNba=-uuuur例2在△ABC中，已知点O满足:，求证：点O是△ABC的重心.0OAOBOC++=uuuruuuruuurOCBADE例3在平行四边形ABCD中，M是AB的中点，点N在BD上，且BD=3BN，试推断点M、N、C是否共线？并说明理由.ABCDMN13MNMC=uuuuruuur例4在Rt△ABC中，已知斜边BC=2，线段PQ以A为中点，且PQ=4，向量与的夹角为60°，求.BCuuurPQuuurBPCQuuuruuurgPCBAQ2BPCQ=-uuuruuurg例5如图，OM//AB，点P在由射线OM、线段OB及AB的延长线围成的区域内（不含边界）运动，且.（1）求x的取值范围；（2）当时，求y的取值范围.OPxOAyOB�12xAOMPB(,0)x13(,)22y作业：P118复习参考题A组：3.P120复习参考题B组：4，5，6.P118复习参考题A组：1，2(做书上)