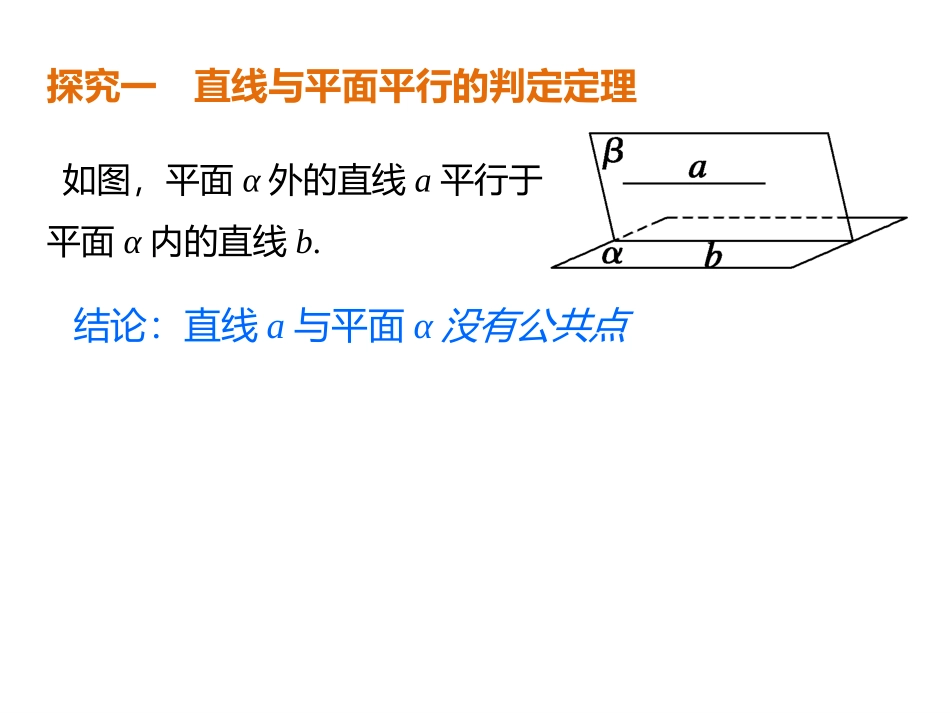
温故知新α∥βa∥α直线和平面没有公共点平面和平面没有公共点定义直线和平面平行平面和平面平行探究一直线与平面平行的判定定理如图,平面α外的直线a平行于平面α内的直线b.结论:直线a与平面α没有公共点文字语言:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.直线与平面平行的判定定理ba∥b.符号语言:a⊄α⇒a∥αb⊂α该定理可以简记为:线线平行⇒线面平行.新课新课//,//,//,,1212121llllll则,若平面)辨析:直线(内直线的关系是与,则平面)填空:如果直线(ll//21l2l2l反例:l答:平行或异面应用举例BCDEFACABFEABCD平面)求证:(的中点分别是中,已知四面体//1,,例1EF几对线面平行的中点,则图中还有分别是若DCBDHG,,)2(DDAABCDCBAABCD1111111//)1(-平面求证:中,正方体例2ABCDEFCBABFE平面的中点,求证分别是已知//:,,)2(11ACDBA1D1C1B1改为三等分点呢?的中点吗?一定得是变式:CBABFE11,,练习1如图所示,在正方体ABCD—A1B1C1D1中,E、F分别是棱BC、C1D1的中点,求证:EF∥平面BDD1B1.ACDMNBCDABDNMABCD平面)求证:(的重心分别是中,已知四面体//1,,练习2文字语言:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.1.直线与平面平行的判定定理ba∥b.符号语言:a⊄α⇒a∥αb⊂α该定理可以简记为:线线平行⇒线面平行.新课复习2.平面与平面平行的判定定理(1)文字语言:⇒β∥α.a∥α,b∥αa⊂β,b⊂βa∩b=P一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.(2)符号语言:简记为:线面平行面⇒面平行.线线平行⇒例2如图,已知正方体ABCD—A1B1C1D1,求证:平面AB1D1∥平面C1BD.证明因为在正方体ABCD—A1B1C1D1中所以D1C1∥AB,D1C1=AB,所以四边形D1C1BA是平行四边形,所以D1A∥C1B,又D1A⊄平面C1BD,C1B⊂平面C1BD,所以D1A∥平面C1BD,同理D1B1∥平面C1BD,所以,平面AB1D1∥平面C1BD.又D1A⊂平面AB1D1D1B1⊂平面AB1D1D1A∩D1B1=D1,例3如图,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、DC、SC的中点,求证:(1)直线EG∥平面BDD1B1;∵E、G分别是BC、SC的中点,∴EG∥SB.又∵SB⊂平面BDD1B1,EG⊄平面BDD1B1,∴直线EG∥平面BDD1B1.证明连接SB,(2)平面EFG∥平面BDD1B1.证明连接SD,∵F、G分别是DC、SC的中点,∴FG∥SD.又∵SD⊂平面BDD1B1,FG⊄平面BDD1B1,EG∩FG=G,∴FG∥平面BDD1B1又∵EG∥平面BDD1B1∴平面EFG∥平面BDD1B1.EG,FG⊂平面EFG,练习如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?解当Q为CC1的中点时,平面D1BQ∥平面PAO.当堂练:1.若A是直线m外一点,过A且与m平行的平面()A.存在无数个B.不存在C.存在但只有一个D.只存在两个2.直线a,b为异面直线,过直线a与直线b平行的平面()A.有且只有一个B.有无数多个C.至多一个D.不存在AA3.下列说法中正确的是()①一个平面内有两条直线都与另外一个平面平行,则这两个平面平行;②一个平面内有无数条直线都与另外一个平面平行,则这两个平面平行;③一个平面内任何直线都与另外一个平面平行,则这两个平面平行;④一个平面内有两条相交直线都与另外一个平面平行,则这两个平面平行.A.①③B.②④C.②③④D.③④D4.如图,P是平行四边形ABCD所在平面外一点,E、F分别是AB、PD的中点.求证:AF∥平面PCE.归纳小结1.判定线面平行的方法:(1)定义法:(2)判定定理:3.判定面面平行的方法:(1)定义法;(2)判定定理:直线与平面没有公共点a∥b.a⊄α⇒a∥αb⊂α平面与平面没有公共点⇒β∥α.a∥α,b∥αa⊂β,b⊂βa∩b=P(3)两个平面同时平行于第三个平面,那么这两个平面平行.线线平行线⇒面平行⇒面面平行.(线面平行面⇒面平行.)