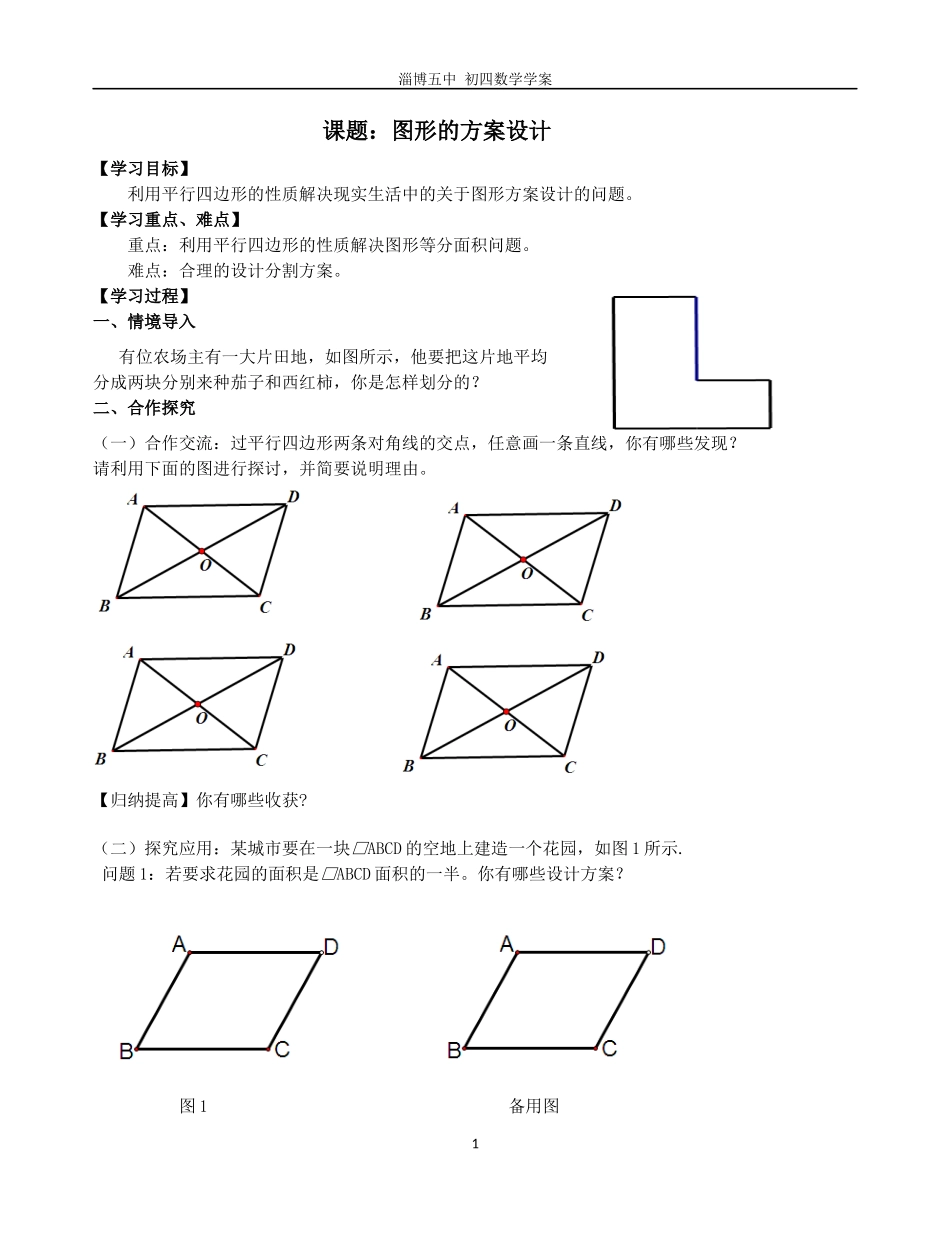
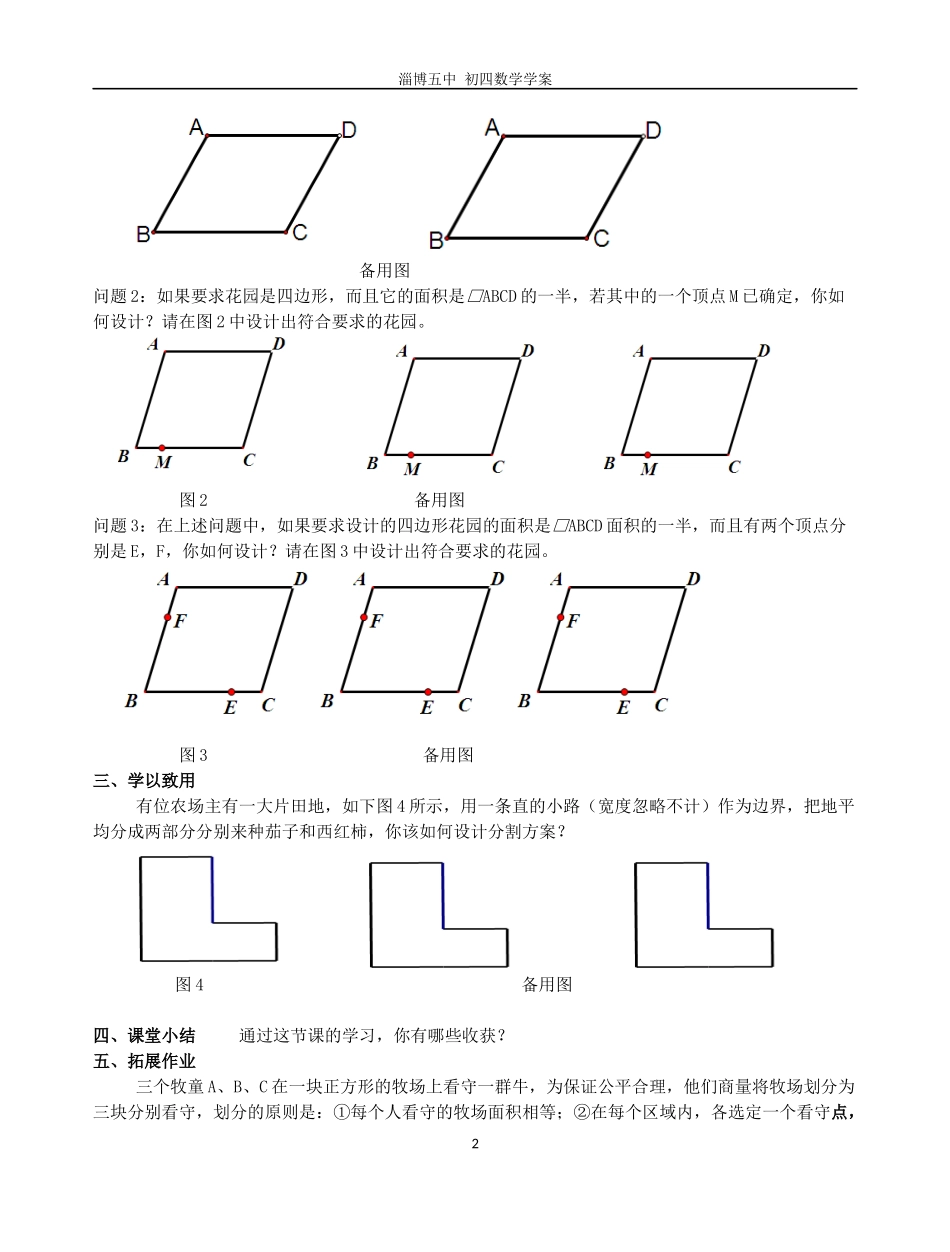
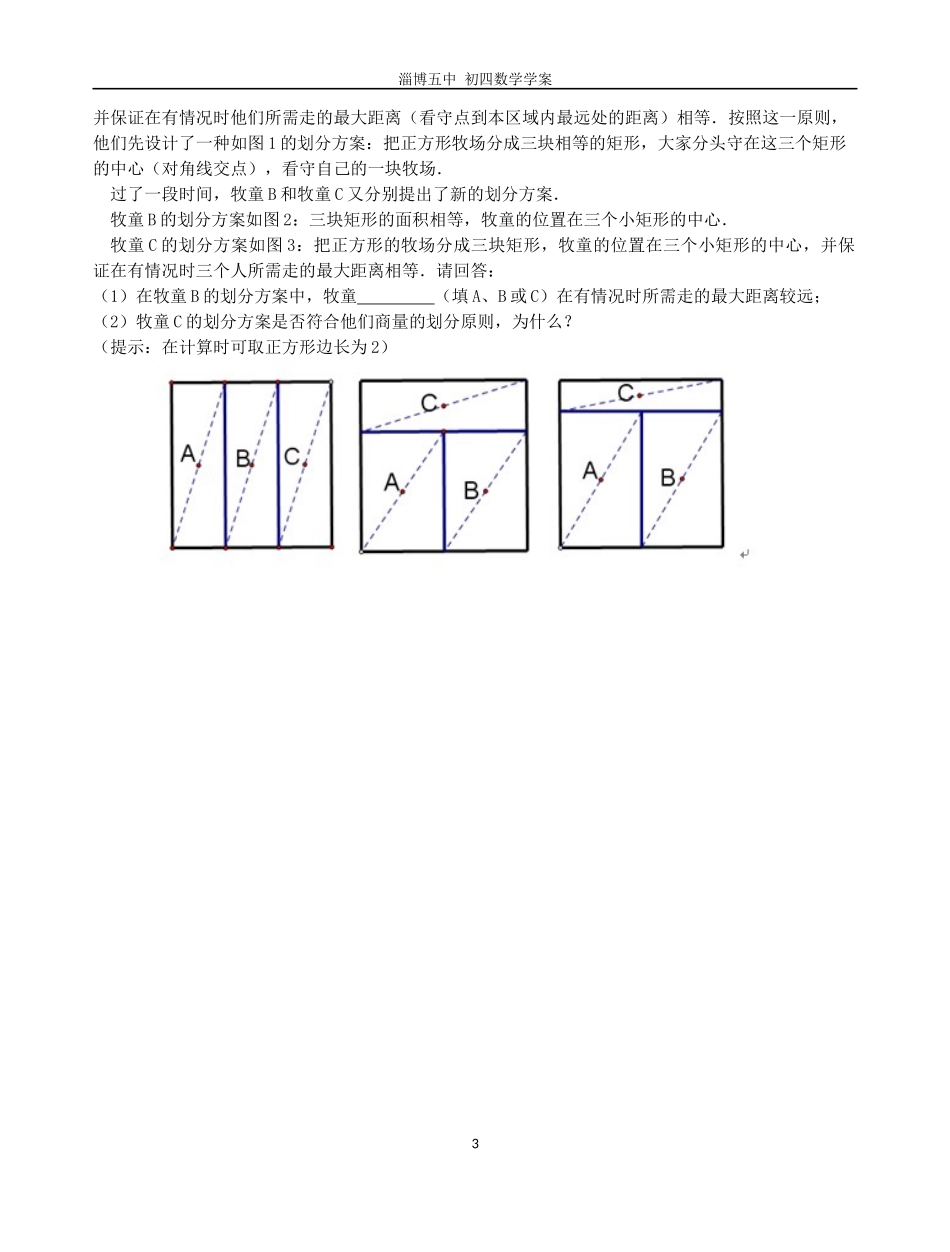
淄博五中初四数学学案课题:图形的方案设计【学习目标】利用平行四边形的性质解决现实生活中的关于图形方案设计的问题。【学习重点、难点】重点:利用平行四边形的性质解决图形等分面积问题。难点:合理的设计分割方案。【学习过程】一、情境导入有位农场主有一大片田地,如图所示,他要把这片地平均分成两块分别来种茄子和西红柿,你是怎样划分的?二、合作探究(一)合作交流:过平行四边形两条对角线的交点,任意画一条直线,你有哪些发现?请利用下面的图进行探讨,并简要说明理由。【归纳提高】你有哪些收获?(二)探究应用:某城市要在一块□ABCD的空地上建造一个花园,如图1所示.问题1:若要求花园的面积是□ABCD面积的一半。你有哪些设计方案?图1备用图1淄博五中初四数学学案备用图问题2:如果要求花园是四边形,而且它的面积是□ABCD的一半,若其中的一个顶点M已确定,你如何设计?请在图2中设计出符合要求的花园。图2备用图问题3:在上述问题中,如果要求设计的四边形花园的面积是□ABCD面积的一半,而且有两个顶点分别是E,F,你如何设计?请在图3中设计出符合要求的花园。图3备用图三、学以致用有位农场主有一大片田地,如下图4所示,用一条直的小路(宽度忽略不计)作为边界,把地平均分成两部分分别来种茄子和西红柿,你该如何设计分割方案?图4备用图四、课堂小结通过这节课的学习,你有哪些收获?五、拓展作业三个牧童A、B、C在一块正方形的牧场上看守一群牛,为保证公平合理,他们商量将牧场划分为三块分别看守,划分的原则是:①每个人看守的牧场面积相等;②在每个区域内,各选定一个看守点,2淄博五中初四数学学案并保证在有情况时他们所需走的最大距离(看守点到本区域内最远处的距离)相等.按照这一原则,他们先设计了一种如图1的划分方案:把正方形牧场分成三块相等的矩形,大家分头守在这三个矩形的中心(对角线交点),看守自己的一块牧场.过了一段时间,牧童B和牧童C又分别提出了新的划分方案.牧童B的划分方案如图2:三块矩形的面积相等,牧童的位置在三个小矩形的中心.牧童C的划分方案如图3:把正方形的牧场分成三块矩形,牧童的位置在三个小矩形的中心,并保证在有情况时三个人所需走的最大距离相等.请回答:(1)在牧童B的划分方案中,牧童(填A、B或C)在有情况时所需走的最大距离较远;(2)牧童C的划分方案是否符合他们商量的划分原则,为什么?(提示:在计算时可取正方形边长为2)3