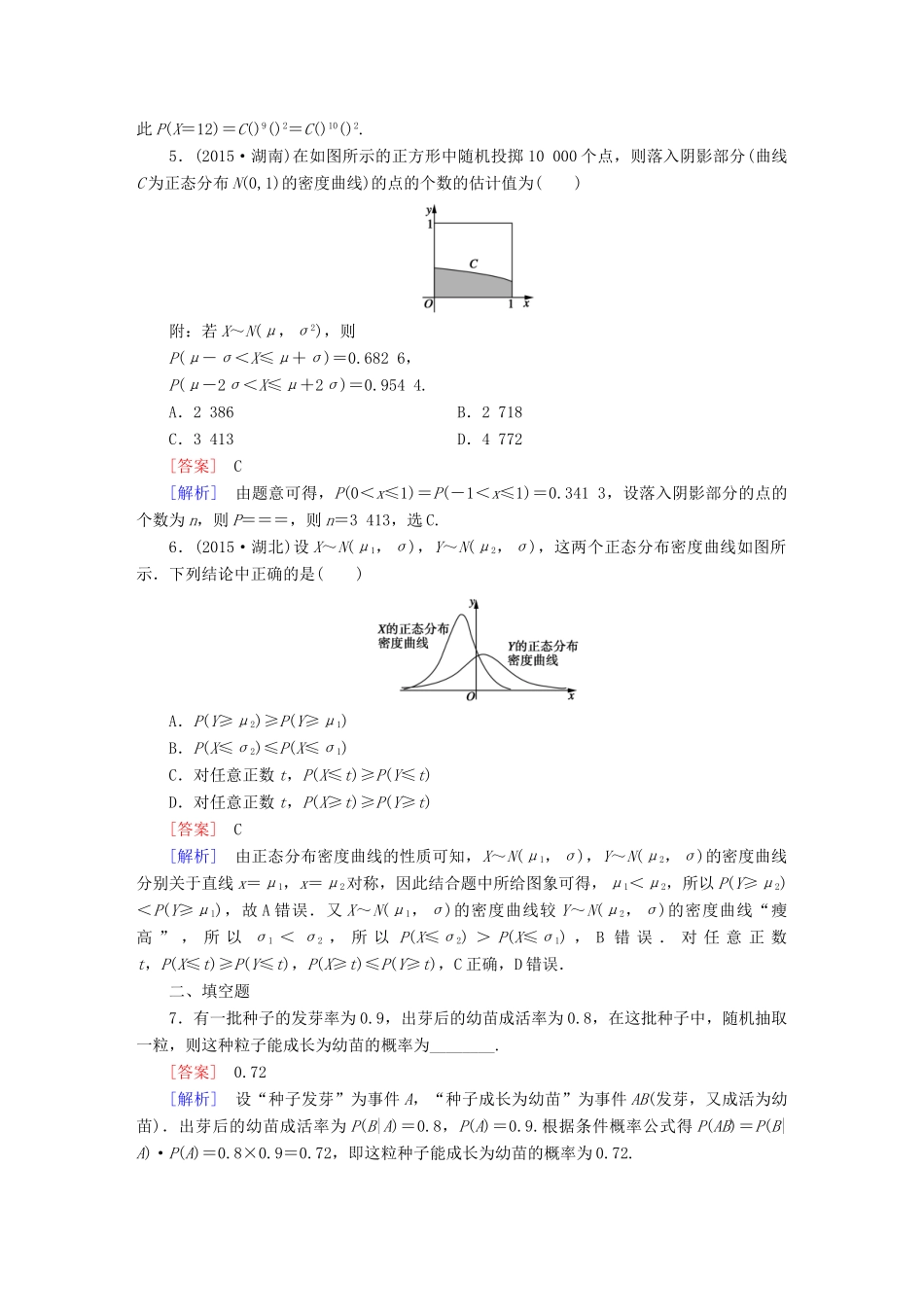
2017高考数学一轮复习第十章计数原理、概率、随机变量第8讲二项分布与正态分布(理)习题A组基础巩固一、选择题1.设由0、1组成的三位编号中,若用A表示“第二位数字为0的事件”,用B表示“第一位数字为0的事件”,则P(A|B)=()A.B.C.D.[答案]A[解析]因为第一位数字可为0或1,所以第一位数字为0的概率P(B)=,第一位数字为0且第二位数字也是0,即事件A,B同时发生的概率P(AB)=×=,所以P(A|B)===.2.(2015·新课标全国Ⅰ)投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为()A.0.648B.0.432C.0.36D.0.312[答案]A[解析]由题意得所求概率P=C×0.62×(1-0.6)+C×0.63=0.648.3.1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球.则从2号箱取出红球的概率是()A.B.C.D.[答案]A[解析]法一:记事件A:最后从2号箱中取出的是红球;事件B:从1号箱中取出的是红球,则根据古典概型和对立事件的概率和为1,可知:P(B)==,P()=1-=;由条件概率公式知P(A|B)==,P(A|)==.从而P(A)=P(AB)+P(A)=P(A|B)·P(B)+P(A|)·P()=,选A.法二:根据题意,分两种情况讨论:①从1号箱中取出白球,其概率为=,此时2号箱中有6个白球和3个红球,从2号箱中取出红球的概率为,则此种情况下的概率为×=.②从1号箱中取出红球,其概率为=.此时2号箱中有5个白球和4个红球,从2号箱取出红球的概率为,则这种情况下的概率为×=.则从2号箱取出红球的概率是+=.4.(2015·长春二模)一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了X次球,则P(X=12)等于()A.C()10()2B.C()9()2C.C()9()2D.C()10()2[答案]D[解析]“X=12”表示第12次取到红球,前11次有9次取到红球,2次取到白球,因此P(X=12)=C()9()2=C()10()2.5.(2015·湖南)在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为()附:若X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544.A.2386B.2718C.3413D.4772[答案]C[解析]由题意可得,P(0<x≤1)=P(-1<x≤1)=0.3413,设落入阴影部分的点的个数为n,则P===,则n=3413,选C.6.(2015·湖北)设X~N(μ1,σ),Y~N(μ2,σ),这两个正态分布密度曲线如图所示.下列结论中正确的是()A.P(Y≥μ2)≥P(Y≥μ1)B.P(X≤σ2)≤P(X≤σ1)C.对任意正数t,P(X≤t)≥P(Y≤t)D.对任意正数t,P(X≥t)≥P(Y≥t)[答案]C[解析]由正态分布密度曲线的性质可知,X~N(μ1,σ),Y~N(μ2,σ)的密度曲线分别关于直线x=μ1,x=μ2对称,因此结合题中所给图象可得,μ1<μ2,所以P(Y≥μ2)<P(Y≥μ1),故A错误.又X~N(μ1,σ)的密度曲线较Y~N(μ2,σ)的密度曲线“瘦高”,所以σ1<σ2,所以P(X≤σ2)>P(X≤σ1),B错误.对任意正数t,P(X≤t)≥P(Y≤t),P(X≥t)≤P(Y≥t),C正确,D错误.二、填空题7.有一批种子的发芽率为0.9,出芽后的幼苗成活率为0.8,在这批种子中,随机抽取一粒,则这种粒子能成长为幼苗的概率为________.[答案]0.72[解析]设“种子发芽”为事件A,“种子成长为幼苗”为事件AB(发芽,又成活为幼苗).出芽后的幼苗成活率为P(B|A)=0.8,P(A)=0.9.根据条件概率公式得P(AB)=P(B|A)·P(A)=0.8×0.9=0.72,即这粒种子能成长为幼苗的概率为0.72.8.甲射击命中目标的概率是,乙命中目标的概率是,丙命中目标的概率是.现在三人同时射击目标,则目标被击中的概率为________.[答案][解析]设甲命中目标为事件A,乙命中目标为事件B,丙命中目标为事件C,则击中目标表示事件A,B,C中至少有一个发生.又P(··)=P()·P()·P()=[1-P(A)]·[1-P(B)]·[1-P(C)]=(1-)(1-)(1-)=.故目标被击中的概率为1-P(··)=1-=.9.在100件产品中有95件合格品,5件不合格品.现从中不放回地取两次,每次任取一次,则在第一次取到不合格品...