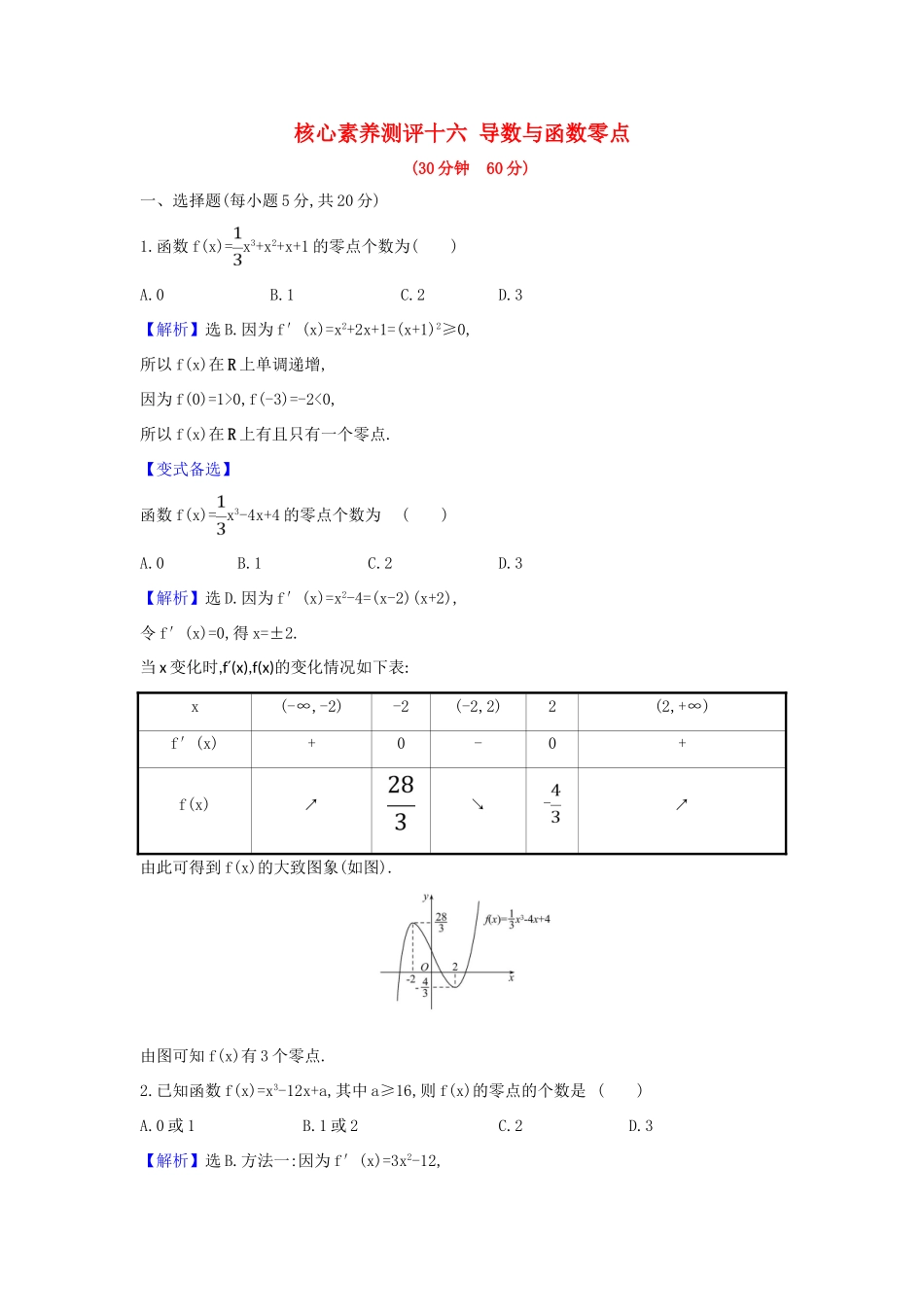
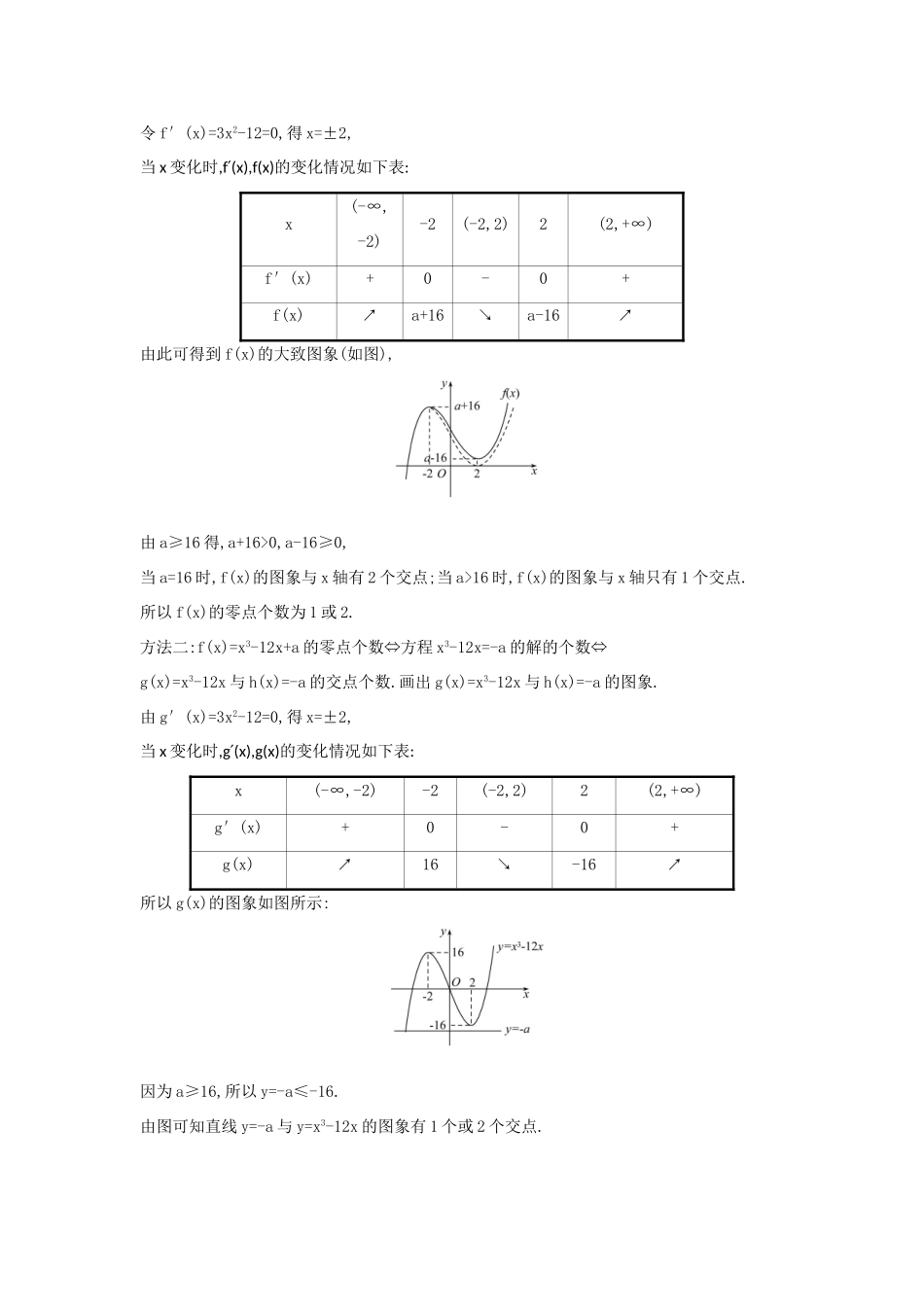
核心素养测评十六导数与函数零点(30分钟60分)一、选择题(每小题5分,共20分)1.函数f(x)=x3+x2+x+1的零点个数为()A.0B.1C.2D.3【解析】选B.因为f′(x)=x2+2x+1=(x+1)2≥0,所以f(x)在R上单调递增,因为f(0)=1>0,f(-3)=-2<0,所以f(x)在R上有且只有一个零点.【变式备选】函数f(x)=x3-4x+4的零点个数为()A.0B.1C.2D.3【解析】选D.因为f′(x)=x2-4=(x-2)(x+2),令f′(x)=0,得x=±2.当x变化时,f(x),f(x)′的变化情况如下表:x(-∞,-2)-2(-2,2)2(2,+∞)f′(x)+0-0+f(x)↗↘-↗由此可得到f(x)的大致图象(如图).由图可知f(x)有3个零点.2.已知函数f(x)=x3-12x+a,其中a≥16,则f(x)的零点的个数是()A.0或1B.1或2C.2D.3【解析】选B.方法一:因为f′(x)=3x2-12,令f′(x)=3x2-12=0,得x=±2,当x变化时,f(x),f(x)′的变化情况如下表:x(-∞,-2)-2(-2,2)2(2,+∞)f′(x)+0-0+f(x)↗a+16↘a-16↗由此可得到f(x)的大致图象(如图),由a≥16得,a+16>0,a-16≥0,当a=16时,f(x)的图象与x轴有2个交点;当a>16时,f(x)的图象与x轴只有1个交点.所以f(x)的零点个数为1或2.方法二:f(x)=x3-12x+a的零点个数⇔方程x3-12x=-a的解的个数⇔g(x)=x3-12x与h(x)=-a的交点个数.画出g(x)=x3-12x与h(x)=-a的图象.由g′(x)=3x2-12=0,得x=±2,当x变化时,g(x),g(x)′的变化情况如下表:x(-∞,-2)-2(-2,2)2(2,+∞)g′(x)+0-0+g(x)↗16↘-16↗所以g(x)的图象如图所示:因为a≥16,所以y=-a≤-16.由图可知直线y=-a与y=x3-12x的图象有1个或2个交点.3.若函数f(x)=恰有2个零点,则a的取值范围为()A.B.∪C.D.∪【解析】选D.当x>0时,令f(x)=0,可得x3-x2-a=0,设g(x)=x3-x2,则g′(x)=x(3x-2),当0时,g′(x)>0,g(x)min=g=-.当x≤0时,令f(x)=0,可得x2+2x-a=0,设h(x)=x2+2x,h(x)min=-1,所以函数f(x)=恰有2个零点,则a的取值范围为∪.4.函数f(x)=ex+a-x3+2x2在(0,+∞)上只有一个零点,则a的值为()A.4B.4ln2-3C.2D.5ln2-4【解析】选D.函数f(x)=ex+a-x3+2x2在(0,+∞)上只有一个零点,可得ea=在(0,+∞)上只有一个解.令g(x)=,可得g′(x)==-x·,在(0,+∞)有2个极值点,x=1和x=4;x∈(0,1)时函数是减函数,x∈(1,4)时,函数是增函数,x∈(4,+∞)时函数是减函数,g(0)=0,所以函数g(x)的最大值为g(4)==,函数f(x)=ex+a-x3+2x2在(0,+∞)上只有一个零点,可得ea=,所以a=5ln2-4.二、填空题(每小题5分,共20分)5.设x3+ax+b=0,其中a,b均为实数,下列条件中,使得该三次方程仅有一个实根的是________.(写出所有正确条件的编号)①a=-3,b=-3;②a=-3,b=2;③a=-3,b>2;④a=0,b=2;⑤a=1,b=2.【解析】令f(x)=x3+ax+b,则f′(x)=3x2+a.当a≥0时,f′(x)≥0,f(x)单调递增,④⑤正确;当a<0时,若a=-3,则f′(x)=3x2-3=3(x+1)(x-1),所以f(x)极大=f(-1)=-1+3+b=b+2,f(x)极小=f(1)=1-3+b=b-2,要使f(x)=0仅有一个实根,需f(x)极大<0或f(x)极小>0,所以b<-2或b>2,①③正确,②不正确.答案:①③④⑤6.(2019·安阳模拟)已知函数f(x)=+与g(x)=6x+a的图象有3个不同的交点,则a的取值范围是________.【解析】原问题等价于函数h(x)=+-6x与函数y=a的图象有3个不同的交点,由h′(x)=x2+x-6=(x-2)(x+3)=0,得x=2或x=-3,当x∈(-∞,-3)时,h′(x)>0,h(x)单调递增;当x∈(-3,2)时,h′(x)<0,h(x)单调递减;当x∈(2,+∞)时,h′(x)>0,h(x)单调递增.且h(-3)=,h(2)=-,数形结合可得a的取值范围是.答案:7.已知函数f(x)=x3+mx+,g(x)=-lnx.min{a,b}表示a,b中的最小值,若函数h(x)=min{f(x),g(x)}(x>0)恰有三个零点,则实数m的取值范围是________.【解析】f′(x)=3x2+m,因为g(1)=0,所以要使h(x)=min{f(x),g(x)}(x>0)恰有三个零点,需满足f(1)>0,f<0,m<0,解得m>-,>⇒-