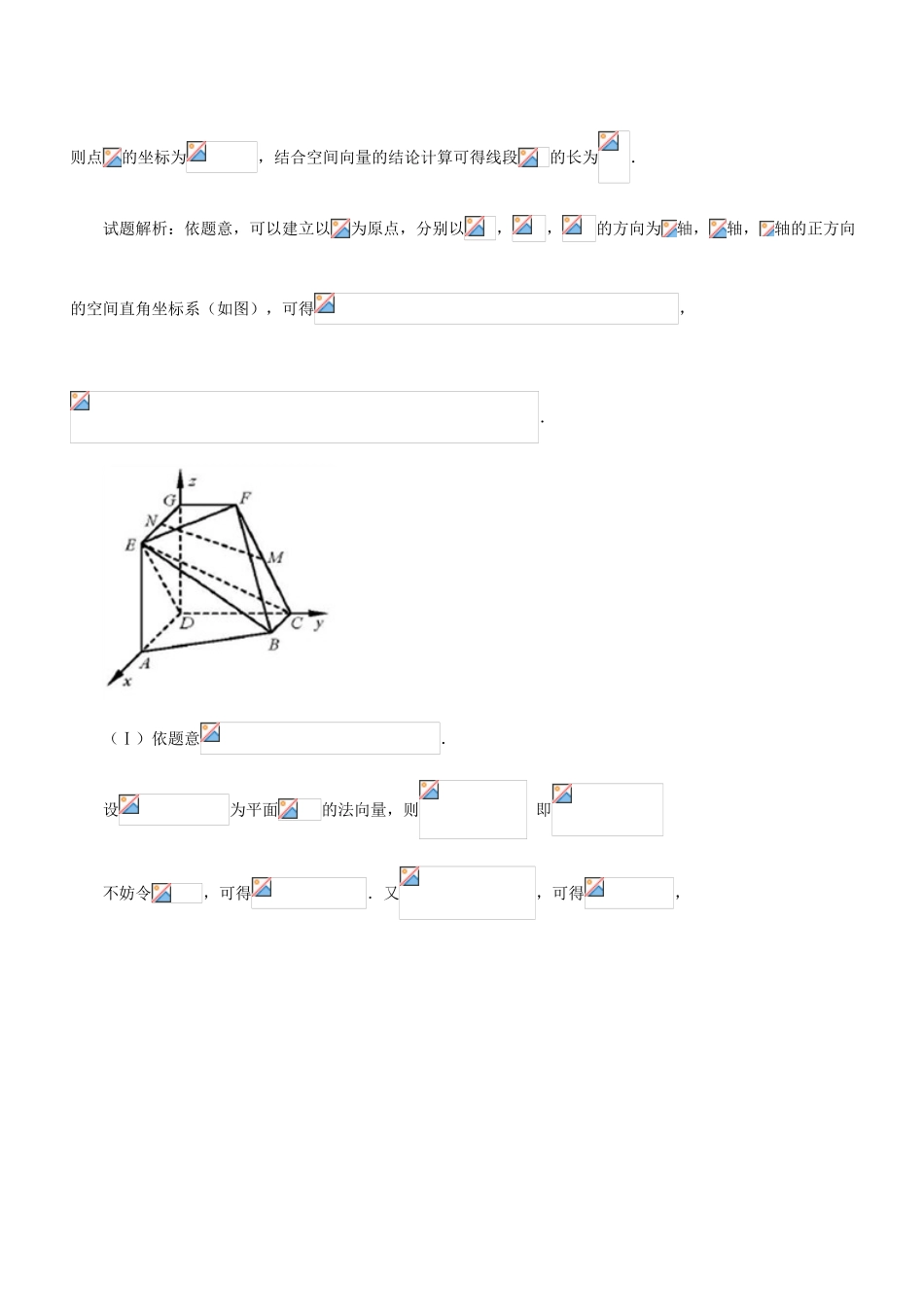
母题十七应用空间向量解决立体几何问题【母题原题1】【2018天津,理17】如图,且AD=2BC,,且EG=AD,且CD=2FG,,DA=DC=DG=2.(I)若M为CF的中点,N为EG的中点,求证:;(II)求二面角的正弦值;(III)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.【考点分析】本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.满分13分.【答案】(I)证明见解析;(II);(III).【解析】试题分析:依题意,可以建立以为原点,分别以,,的方向为轴,轴,则点的坐标为,结合空间向量的结论计算可得线段的长为.试题解析:依题意,可以建立以为原点,分别以,,的方向为轴,轴,轴的正方向的空间直角坐标系(如图),可得,.(Ⅰ)依题意.设为平面的法向量,则即不妨令,可得.又,可得,不妨令,可得.因此有,于是.所以,二面角的正弦值为.(Ⅲ)设线段的长为,则点的坐标为,可得.易知,为平面的一个法向量,故,由题意,可得,解得.所以线段的长为.【名师点睛】本题主要考查空间向量的应用,线面平行的证明,二面角问题等知识,意在考查学生的转化能力和计算求解能力.【母题原题2】【2017天津,理17】如图,在三棱锥P-ABC中,PA⊥底面ABC,.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.(Ⅰ)求证:MN∥平面BDE;(Ⅱ)求二面角C-EM-N的正弦值;(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为,求线段AH的长.【答案】(1)证明见解析;(2);(3)或.试题解析:如图,以A为原点,分别以,,方向为x轴、y轴、z轴正方向建立空间直角坐标系.依题意可得A(0,0,0),B(2,0,0),C(0,4,0),P(0,0,4),D(0,0,2),E(0,2,2),M(0,0,1),N(1,2,0).(Ⅰ)证明:=(0,2,0),=(2,0,).设,为平面BDE的法向量,则,即.不妨设,可得.又=(1,2,),可得. 平面BDE,∴MN//平面BDE.(Ⅱ)易知为平面CEM的一个法向量.设为平面EMN的法向量,则∴线段AH的长为或.【考点】直线与平面平行、二面角、异面直线所成的角【名师点睛】空间向量是解决空间几何问题的锐利武器,不论是求空间角、空间距离还是证明线面关系利用空间向量都很方便,利用向量夹角公式求异面直线所成的角又快又准,特别是借助平面的法向量求线面角,二面角或点到平面的距离都很容易.【母题原题3】【2016天津,理17】如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(I)求证:EG∥平面ADF;(II)求二面角O-EF-C的正弦值;(III)设H为线段AF上的点,且AH=HF,求直线BH和平面CEF所成角的正弦值.【答案】(Ⅰ)详见解析;(Ⅱ);(Ⅲ)..IzyxABCDEFGHO(I)证法1:依题意,.设为平面的法向量,则,即.不妨设,可得,又,可得,又因为直线,所以.证法2:建立如上右图的坐标系来证(略).证法3:找到中点,连结, 矩形,∴. 、是中点,∴是的中位线,∴且. 是正方形中心,∴,∴且,∴四边形是平行四边形,∴. 面,∴面.(II)解法1:易证,为平面的一个法向量.依题意,.设为平面的法向量,则,即.不妨设,可得.因此有,于是,所以,二面角的正弦值为.(III)解:由,得.因为,所以,进而有,从而,因此.所以,直线.考点:利用空间向量解决立体几何问题【名师点睛】1.利用数量积解决问题的两条途径:一是根据数量积的定义,利用模与夹角直接计算;二是利用坐标运算.2.利用数量积可解决有关垂直、夹角、长度问题.(1)a≠0,b≠0,a⊥b⇔a·b=0;(2)|a|=;(3)cos〈a,b〉=.【母题原题4】【2015天津,理】如图,在四棱柱中,侧棱,,,,且点M和N分别为的中点.(I)求证:;(II)求二面角的正弦值;(III)设E为棱上的点,若直线NE和平面ABCD所成角的正弦值为,求线段的长【答案】(I)见解析;(II);(III).【解析】别为和的中点,得.(I)证明:依题意,可得为平面的一个法向量,,由此可得,,又因为直线平面,所以平面(II),...