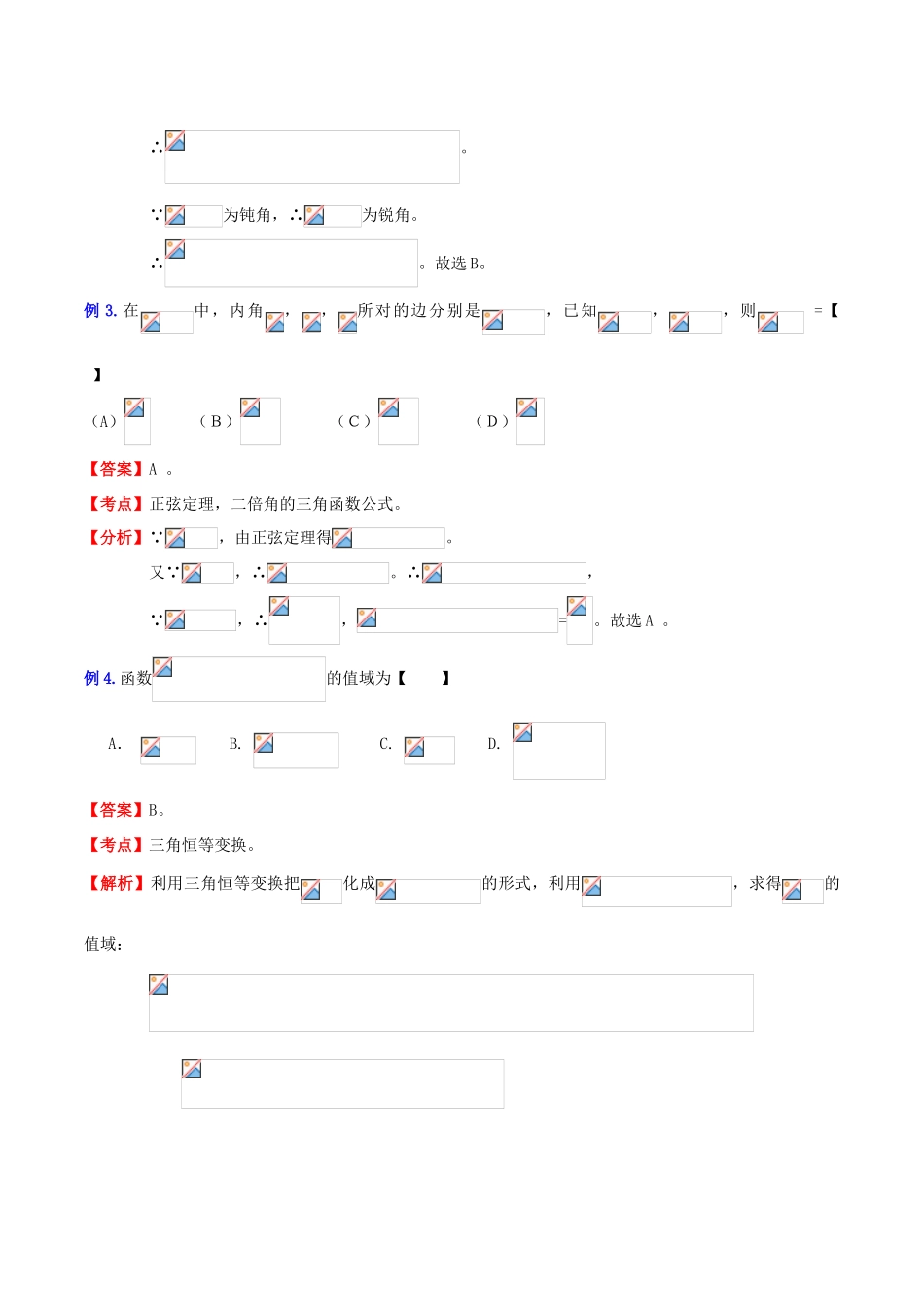
四、三角函数的综合问题:典型例题:例1.若函数是偶函数,则=【】A.B.C.D.【答案】C。【考点】偶函数的性质,和的三角函数公式。【解析】∵函数是偶函数,∴,即。展开,得,即,即。∴,解得。又∵,∴。故选C。例2.如图,正方形的边长为,延长至,使,连接、则【】DCAEBA、B、C、D、【答案】B。【考点】余弦定理,同角函数关系式。【解析】∵,正方形的边长为,∴。∴。∵为钝角,∴为锐角。∴。故选B。例3.在中,内角,,所对的边分别是,已知,,则=【】(A)(B)(C)(D)【答案】A。【考点】正弦定理,二倍角的三角函数公式。【分析】∵,由正弦定理得。又∵,∴。∴,∵,∴,=。故选A。例4.函数的值域为【】A.B.C.D.【答案】B。【考点】三角恒等变换。【解析】利用三角恒等变换把化成的形式,利用,求得的值域:∵,∴。∴函数的值域为。故选B。例5.当函数取得最大值时,▲。【答案】。【考点】三角函数性质的运用。【解析】求解值域的问题,首先化为单一三角函数,然后利用定义域求解角的范围,从而结合三角函数图像得到最值点。∵,∴。∵,∴当且仅当即时,函数取得最大值。例6.设的内角的对边分别为,且则▲【答案】。【考点】同角三角函数的基本关系式,两角和的三角公式,正弦定理的应用。【分析】∵,∴。∵,∴。∴。由正弦定理得,。例7.设△的内角的对边分别为,且,则▲【答案】。【考点】同角三角函数间的基本关系,余弦定理应用,等腰三角形的性质。【分析】由为三角形的内角,及cos的值,利用同角三角函数间的基本关系求出sin的值,再由与的值,利用余弦定理列出关于的方程,求出方程的解得到的值,再由sin,及的值,利用正弦定理即可求出的值:∵为三角形的内角,,∴。又∵,∴由余弦定理得:,解得:。又∵,,,∴由等腰三角形等边对等角的性质得:。(或用正弦定理求解)例8.的内角的对边分别为,已知,求。【答案】解:∵,∴。由正弦定理及可得①,∴。由得②。将①代入②,得,∴。∵为三角形的内角且,∴。∴。∴。【考点】解三角形的运用,三角形的内角和定理,正弦定理,和与差的三角函数。【解析】给出两个公式,一个是边的关系,一个角的关系,而求解的为角,因此要找到角的关系式为好。先将三角函数关系式化简后,得到角关系,然后结合,得到两角的二元一次方程组,自然很容易得到角的值。