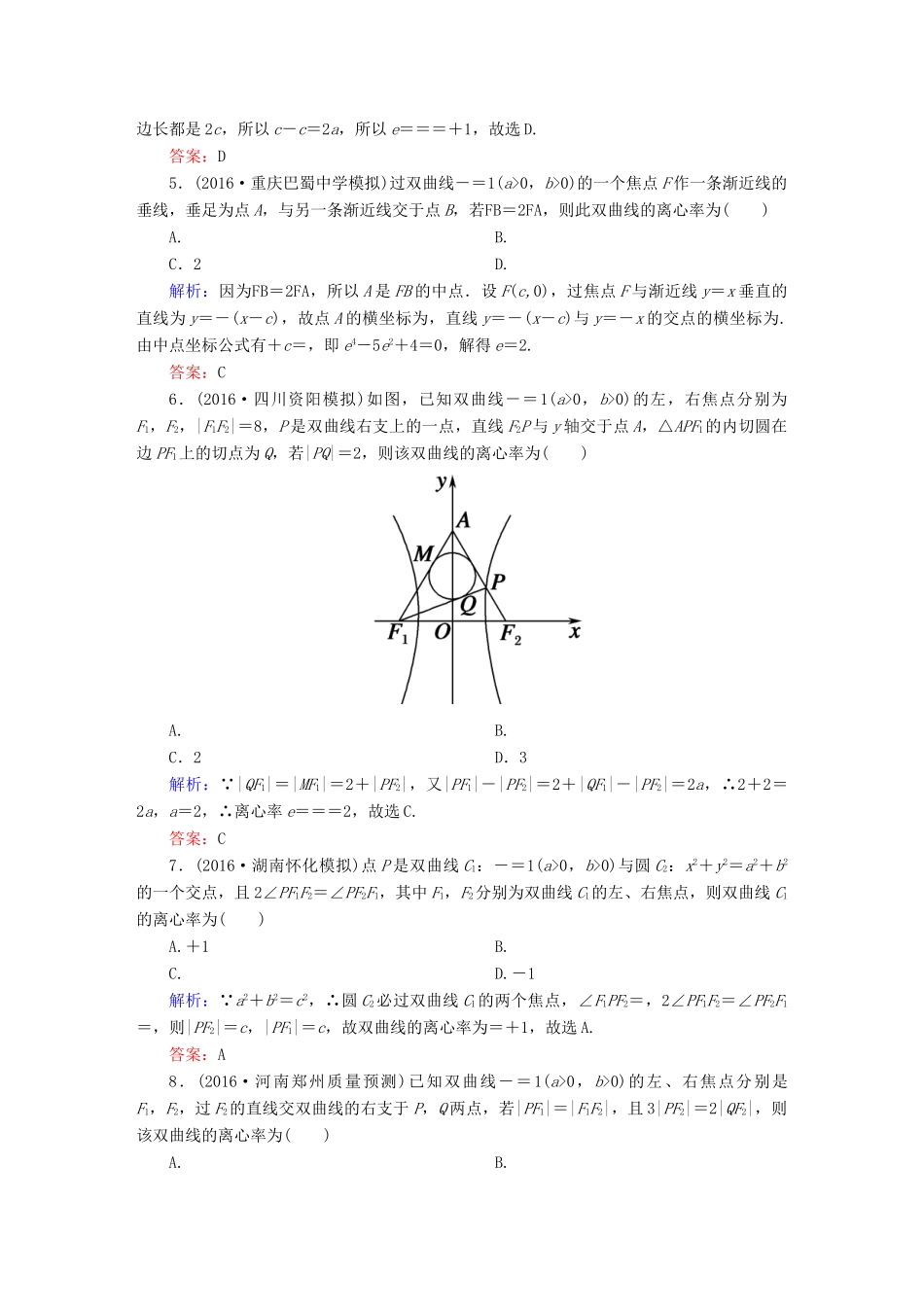
课时作业48双曲线一、选择题1.设双曲线mx2+ny2=1的一个焦点与抛物线y=x2的焦点相同,离心率为2,则此双曲线的方程为()A.x2-=1B.y2-=1C.-=1D.-=1解析:因为抛物线y=x2的焦点为(0,2),双曲线离心率为2,所以c=2,a=1,=a2=1,=-b2=-3,因此n=1,m=-,双曲线方程为y2-=1.答案:B2.已知双曲线C:-=1(a>0,b>0)的焦点为F1,F2,且C上点P满足PF1·PF2=0,|PF1|=3,|PF2|=4,则双曲线C的离心率为()A.B.C.D.5解析:依题意得2a=|PF2|-|PF1|=1. PF1·PF2=0,∴PF1⊥PF2,∴|F1F2|==5,因此该双曲线的离心率e==5,故选D.答案:D3.如图,F1,F2是双曲线-=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的两个分支分别交于点A,B,若△ABF2为等边三角形,则该双曲线的离心率为()A.B.C.4D.解析:点A,B是双曲线上的点,所以,|AF1|-|AF2|=2a, △ABF2为等边三角形,∴|AB|=|AF2|=|BF2|,∴|AF1|-|AB|=|BF1|=2a, |BF2|-|BF1|=2a,∴|BF2|=4a,∠F1BF2=120°,|F1F2|=2c,∴根据余弦定理得|F1F2|2=|BF1|2+|BF2|2-2|BF1|·|BF2|·cos∠F1BF2,将数据代入得4c2=(2a)2+(4a)2-2·2a·4a·cos120°,整理得c2=7a2,e2==7,e=,故选D.答案:D4.(2016·广西南宁五校联考)已知F1,F2是双曲线-=1(a>0,b>0)的两焦点,以线段F1F2为边作正三角形MF1F2.若边MF1的中点P在双曲线上,则双曲线的离心率为()A.4+2B.-1C.D.+1解析:因为MF1的中点P在双曲线上,所以|PF2|-|PF1|=2a.因为△MF1F2为正三角形,边长都是2c,所以c-c=2a,所以e===+1,故选D.答案:D5.(2016·重庆巴蜀中学模拟)过双曲线-=1(a>0,b>0)的一个焦点F作一条渐近线的垂线,垂足为点A,与另一条渐近线交于点B,若FB=2FA,则此双曲线的离心率为()A.B.C.2D.解析:因为FB=2FA,所以A是FB的中点.设F(c,0),过焦点F与渐近线y=x垂直的直线为y=-(x-c),故点A的横坐标为,直线y=-(x-c)与y=-x的交点的横坐标为.由中点坐标公式有+c=,即e4-5e2+4=0,解得e=2.答案:C6.(2016·四川资阳模拟)如图,已知双曲线-=1(a>0,b>0)的左,右焦点分别为F1,F2,|F1F2|=8,P是双曲线右支上的一点,直线F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=2,则该双曲线的离心率为()A.B.C.2D.3解析: |QF1|=|MF1|=2+|PF2|,又|PF1|-|PF2|=2+|QF1|-|PF2|=2a,∴2+2=2a,a=2,∴离心率e===2,故选C.答案:C7.(2016·湖南怀化模拟)点P是双曲线C1:-=1(a>0,b>0)与圆C2:x2+y2=a2+b2的一个交点,且2∠PF1F2=∠PF2F1,其中F1,F2分别为双曲线C1的左、右焦点,则双曲线C1的离心率为()A.+1B.C.D.-1解析: a2+b2=c2,∴圆C2必过双曲线C1的两个焦点,∠F1PF2=,2∠PF1F2=∠PF2F1=,则|PF2|=c,|PF1|=c,故双曲线的离心率为=+1,故选A.答案:A8.(2016·河南郑州质量预测)已知双曲线-=1(a>0,b>0)的左、右焦点分别是F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为()A.B.C.2D.解析:由题意得|PF1|=|F1F2|=2c,由双曲线的定义|PF2|=2c-2a.又因为3|PF2|=2|QF2|,所以|QF2|=3c-3a,则|QF1|=3c-a.因为∠PF2F1=π-∠QF2F1,所以cos∠PF2F1=-cos∠QF2F1,由余弦定理的推论得=-,化简并整理得5c2-12ac+7a2=0,即5e2-12e+7=0,解得e=或e=1(舍去).故选A.答案:A9.(2016·河南豫东、豫北十校测试)双曲线C:-=1(a>0,b>0)的一条渐近线与直线x+2y+1=0垂直,F1,F2分别为C的左、右焦点,A为双曲线上一点,若|F1A|=2|F2A|,则cos∠AF2F1=()A.B.C.D.解析:因为双曲线的一条渐近线与直线x+2y+1=0垂直,所以b=2a.又|F1A|=2|F2A|,且|F1A|-|F2A|=2a,所以|F2A|=2a,|F1A|=4a,而c2=5a2,即2c=2a,所以cos∠AF2F1===,故选C.答案:C10.(2016·湖北黄冈调研)点P是双曲线-=1(a>0,b>0)左支上的一点,其右焦点为F(c,0),若M为线段FP的中点,且M到坐标原点的距离为,则双曲线的离心率e的取值范围是()A.B.(1,8]C.D.(2,3]解析...