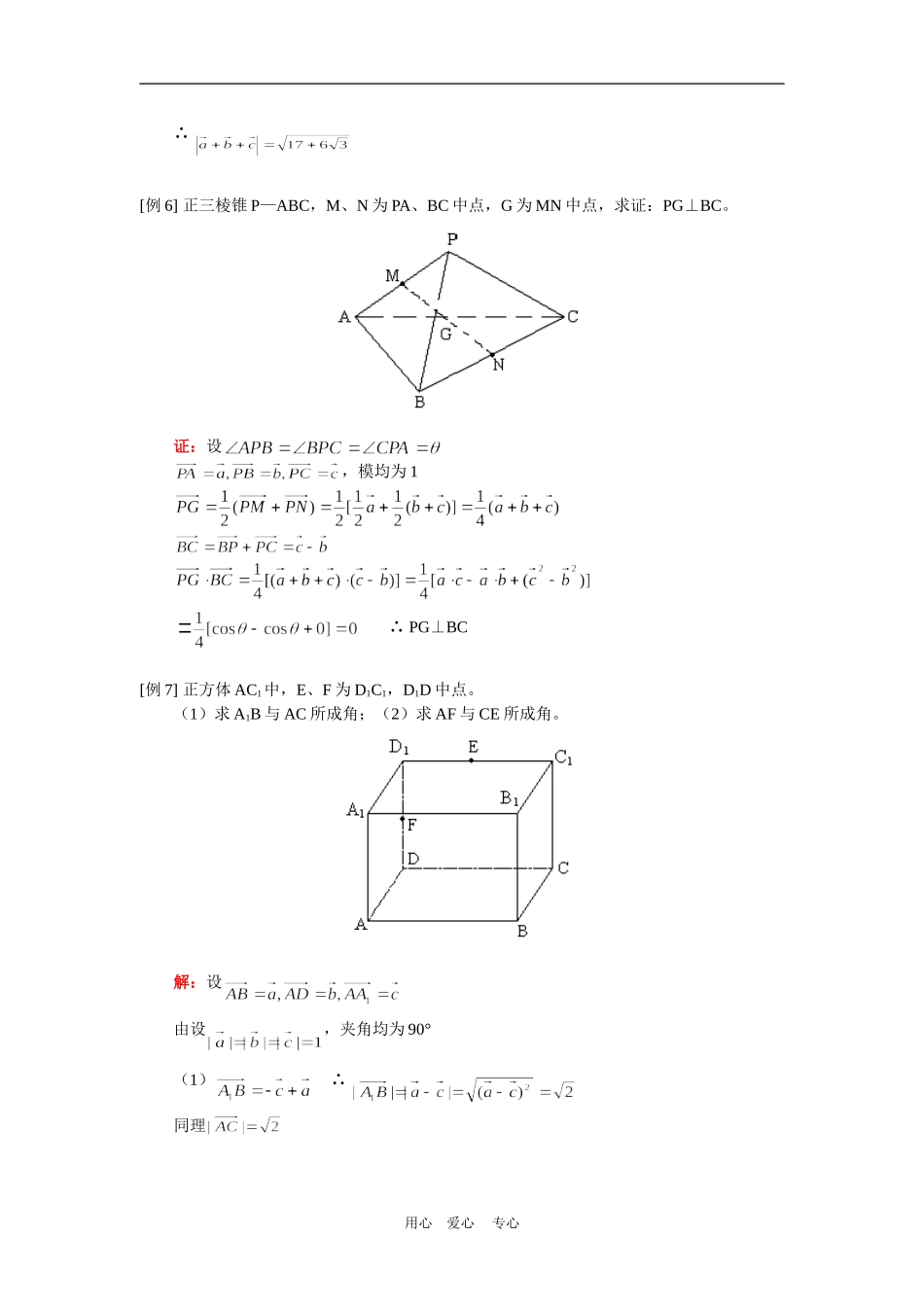
高二数学(理)空间向量及其运算人教实验版(A)【本讲教育信息】一.教学内容:空间向量及其运算二.重点、难点:1.在同一个平面内平面向量的所有结论均可使用。2.A、B、C三点共线3.共面向量均在平面内(x,y唯一)4.空间向量的坐标表示(1)(2)(3)【典型例题】[例1]已知,且,,,求证:A、B、D三点共线。解:A、B、D三点共线∴A、B、D三点共线[例2]已知,如果,,,求证:A、B、C、D四点共面。解:A、B、C、D四点共面∴∴A、B、C、D四点共面[例3]空间不共面四点O、A、B、C,点P满足,求证:P、A、B、C四点共面。用心爱心专心证:∵∴∴P、A、B、C四点共面结论:O、A、B、C空间不共面四点P、A、B、C四点共面且[例4]正方体AC1中,M为DD1中点,N在AC上,,求证:A1、M、N、B四点共面证:∴∴∴、M、N、B四点共面[例5]已知夹角夹角,且,求的模。解:用心爱心专心∴[例6]正三棱锥P—ABC,M、N为PA、BC中点,G为MN中点,求证:PG⊥BC。证:设,模均为1∴PG⊥BC[例7]正方体AC1中,E、F为D1C1,D1D中点。(1)求A1B与AC所成角;(2)求AF与CE所成角。解:设由设,夹角均为90°(1)∴同理用心爱心专心∴(2)[例8]四面体P—ABC中,PA⊥BC,PB⊥AC,求证:PC⊥AB。证:∴PC⊥AB[例9](1)若,求;(2)若,求。解:(1)∴∴∴(2)∴∴[例10]A(1,0,1)B(4,4,6)C(2,2,3)D(10,14,17),求证A、B、C、D四点共面。解:∴∴用心爱心专心∴共面∴A、B、C、D共面。[例11],求:。解:∵∴,∴[例12]正方体AC1中棱长为1,E、F为D1D,BD中点,G在CD上,且,H为C1G中点。(1)求证:EF⊥B1C;(2)EF与C1G所成角的余弦;(3)求FH的长;(4)E到面AB1C的距离。解:建立坐标系∴A(1,0,0)E(0,0,)F(,,0)C(0,1,0)C1(0,1,1)B(1,1,0)G(0,,0)解:(1)∴EF⊥B1C(2)用心爱心专心(3)(4)过E作EQ⊥面AB1C于Q∴且∴,∴∴,∴【模拟试题】1.若为任意向量,,下列等式不一定成立的是()A.B.C.D.2.若向量夹角的余弦值为,则等于()A.2B.-2C.-2或D.2或3.空间四点A、B、C、D每两点的连线长都等于a,动点P在线段AB上,动点Q在线段CD上,则点P与Q的最小距离为()A.B.C.D.4.在以下命题中,不正确的个数为()①是共线的充要条件②若,则存在唯一的实数,使③对空间任意一点O和不共线的三点A、B、C,若,则P、A、B、C四点共面④若为空间的一个基底,则构成空间的另一个基底⑤A.2B.3C.4D.55.设,且,则等于()A.-4B.9C.-9D.6.在正三棱柱ABC—A1B1C1中,若,则与所成角的大小为()A.60°B.90°C.105°D.75°7.在中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离是()A.B.C.D.用心爱心专心8.一条长为的线段,夹在互相垂直的两个平面之间,它和这两个平面所成的角分别是45°和30°,由这条线段两端向两平面的交线引垂线,垂足间的距离是()A.B.C.D.9.正方体的棱长为,E、F分别是BB1、CD的中点,则点F到平面A1D1E的距离为()A.B.C.D.10.已知平行六面体中,ABCD是边长为的正方形,,,则AC1的长=。11.已知,向量与轴垂直,且满足,则。12.在长方体中,和与底面所成的角分别为60°和45°,则异面直线和所成角的余弦值为。用心爱心专心【试题答案】1.D2.C3.B4.C5.B6.B7.B8.A9.C10.11.12.用心爱心专心