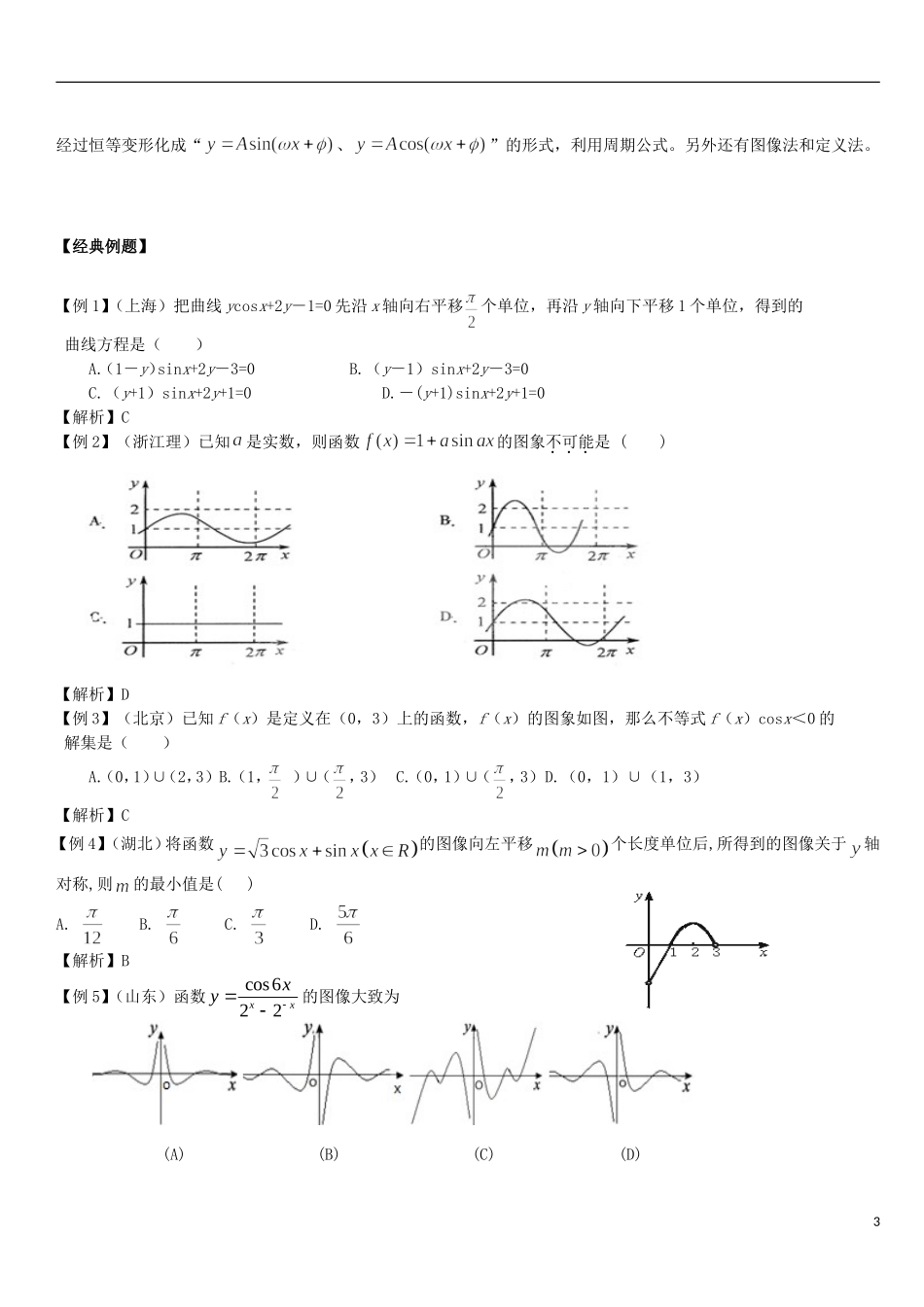
三角函数的图像与性质【考纲说明】1.能画出y=sinx,y=cosx,y=tanx的图像,了解三角函数的周期性;2.借助图像理解正弦函数、余弦函数在[0,2π],正切函数在(-π/2,π/2)上的性质(如单调性、最大和最小值、周期性、图像与x轴交点等);3.结合具体实例,了解的实际意义;【知识梳理】一、三角函数的图像与性质1、正弦函数、余弦函数和正切函数的图象与性质:图象定义域值域最值当时,;当时,.当时,;当时,.既无最大值也无最小值周期性奇偶性奇函数偶函数奇函数单调性在在上是增函数;在在1函数性质上是增函数;在上是减函数.上是减函数.上是增函数.对称性对称中心对称轴对称中心对称轴对称中心无对称轴2、函数的性质振幅:;最大值是,最小值是,周期是,频率是,相位是,初相是;其图象的对称轴是直线,凡是该图象与直线的交点都是该图象的对称中心。二、三角函数图像的变换1、五点法作y=Asin(ωx+)的简图:五点取法是设t=ωx+,由t取0、、π、、2π来求相应的x值及对应的y值,再描点作图。五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).2、三角函数的图像变换三角函数的图象变换有振幅变换、周期变换和相位变换等.由y=sinx的图象利用图象变换作函数y=Asin(ωx+φ)(A>0,ω>0)(x∈R)的图象。注意:当周期变换和相位变换的先后顺序不同时,原图象延x轴量伸缩量的区别。三、三角函数中解题常用方法1、由y=sinx的图象变换出y=Asin(ωx+)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。途径一:先平移变换(相位变换),再周期变换(横向伸缩变换),最后振幅变换(纵向伸缩变换);途径二:先周期变换(横向伸缩变换),再平移变换(相位变换),最后振幅变换(纵向伸缩变换)。2、由y=Asin(ωx+)的图象求其函数式:(图像或性质)确定解析式y=Asin(ωx+)的题型,通常先通最值确定,再有周期确定,最后代入某个中心点坐标来完成确定。3、由变换出、、的图像,并注意变换后周期的变化。4、求三角函数的周期的常用方法:2经过恒等变形化成“、”的形式,利用周期公式。另外还有图像法和定义法。【经典例题】【例1】(上海)把曲线ycosx+2y-1=0先沿x轴向右平移个单位,再沿y轴向下平移1个单位,得到的曲线方程是()A.(1-y)sinx+2y-3=0B.(y-1)sinx+2y-3=0C.(y+1)sinx+2y+1=0D.-(y+1)sinx+2y+1=0【解析】C【例2】(浙江理)已知是实数,则函数的图象不可能是()【解析】D【例3】(北京)已知f(x)是定义在(0,3)上的函数,f(x)的图象如图,那么不等式f(x)cosx<0的解集是()A.(0,1)∪(2,3)B.(1,)∪(,3)C.(0,1)∪(,3)D.(0,1)∪(1,3)【解析】C【例4】(湖北)将函数的图像向左平移个长度单位后,所得到的图像关于轴对称,则的最小值是()A.B.C.D.【解析】B【例5】(山东)函数cos622xxxy的图像大致为(A)(B)(C)(D)3【解析】D【例6】Error:Referencesourcenotfound(山东)将函数的图象沿轴向左平移个单位后,得到一个偶函数的图象,则的一个可能取值为()A.B.C.0D.【解析】B【例7】(全国新课标)已知,函数在上单调递减.则的取值范围是()A.B.C.D.【解析】A【例8】(2013上海)已知函数,其中常数;(1)若在上单调递增,求的取值范围;(2)令,将函数的图像向左平移个单位,再向上平移1个单位,得到函数的图像,区间(且)满足:在上至少含有30个零点,在所有满足上述条件的中,求的最小值.【解析】(1)因为,根据题意有(2),或,即的零点相离间隔依次为和,故若在上至少含有30个零点,则的最小值为【例9】已知函数,.(1)求的最大值和最小值;4(2)在上恒成立,求实数的取值范围.【解析】(Ⅰ).(Ⅱ)的取值范围是.【例10】(山东)已知向量(sin,1)mx�,(3cos,cos2)(0)2AnAxxA,函数()fxmn�的最大值为6.(Ⅰ)求A;(Ⅱ)将函数()yfx的图象向左平移个单位,再将所得图象各点的横坐标缩短为原来的,纵坐标不变,得到函数()ygx的图象,求()gx在5[0,]24上的值域.【解析】(Ⅰ);(Ⅱ)g(x)在上的值域为.【例11】(2012湖北)已知向量a=,b=,设函数f(x)=a·b+的图...