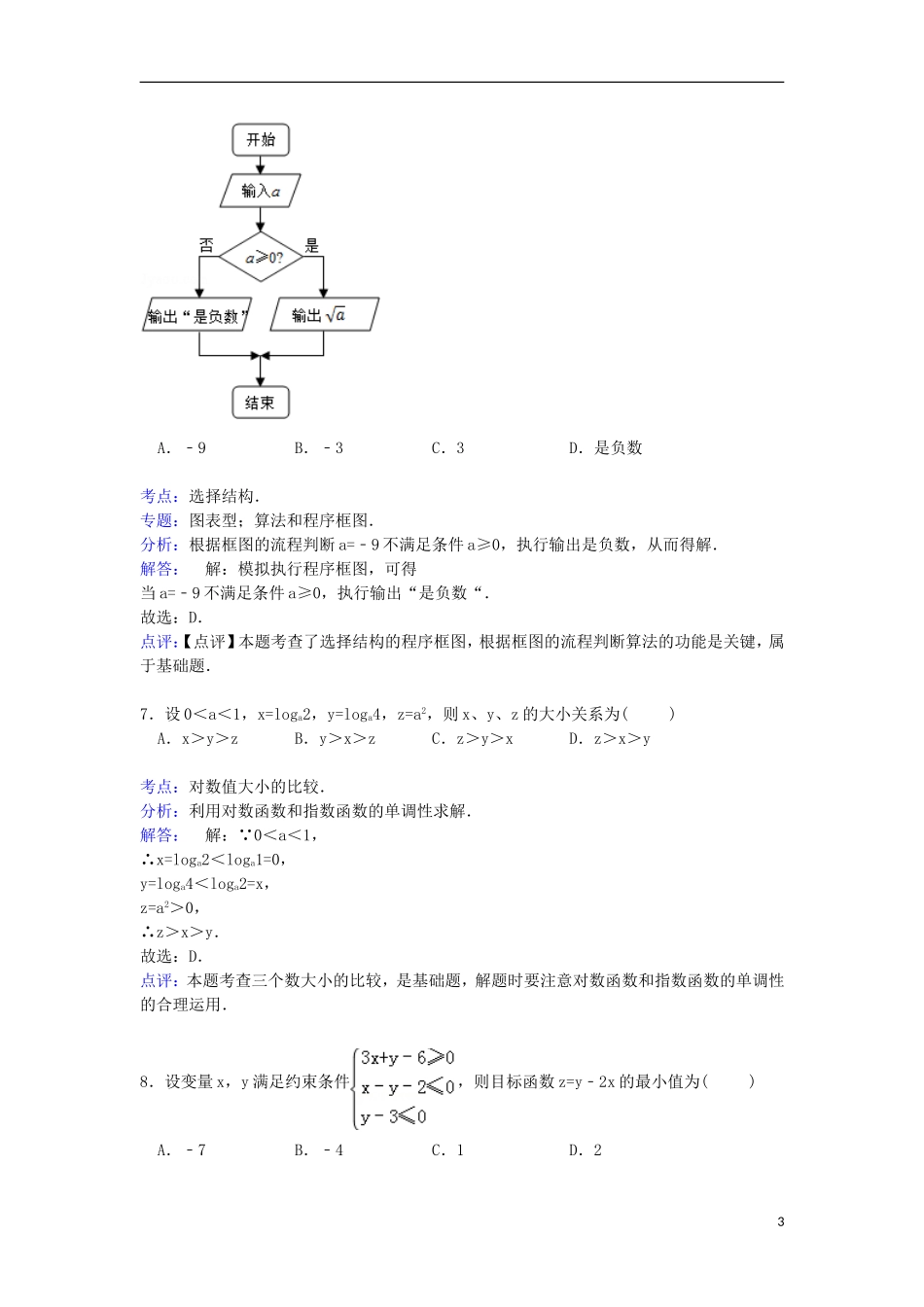
福建省宁德市2014-2015学年高二下学期期末数学试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一个项是符合题目要求的.1.设全集U={1,3,5,7,9},A={1,5,9},B={3,7,9},则(∁UA)∩B=()A.{3}B.{7}C.{3,7}D.∅考点:交、并、补集的混合运算.专题:集合.分析:由条件和补集的运算求出∁UAB,由交集的运算求出(∁UA)∩B.解答:解: 全集U={1,3,5,7,9},A={1,5,9},∴∁UA={3,7},又B={3,7,9},∴(∁UA)∩B={3,7},故选:C.点评:本题考查交、并、补集的混合运算,属于基础题.2.用三段论推理:“任何实数的平方大于0,因为a是实数,所以a2>0”,你认为这个推理()A.大前提错误B.小前提错误C.推理形式错误D.是正确的考点:演绎推理的基本方法.专题:常规题型.分析:要分析一个演绎推理是否正确,主要观察所给的大前提,小前提和结论是否都正确,根据三个方面都正确,得到结论.解答:解: 任何实数的平方大于0,因为a是实数,所以a2>0,大前提:任何实数的平方大于0是不正确的,0的平方就不大于0.故选A.点评:本题是一个简单的演绎推理,这种问题不用进行运算,只要根据所学的知识点,判断这种说法是否正确,是一个基础题.3.如图是解决数学问题的思维过程的流程图:图中①、②两条流程线与“推理与证明”中的思维方法相匹配是()A.①﹣分析法,②﹣综合法B.①﹣综合法,②﹣分析法C.①﹣综合法,②﹣反证法D.①﹣分析法,②﹣反证法考点:分析法和综合法.专题:证明题;推理和证明.分析:根据综合法和分析法的定义,可知由已知到可知进而得到结论的应为综合法,由未知到需知,进而找到与已知的关系为分析法,进而得到答案.1解答:解:根据已知可得该结构图为证明方法的结构图: 由已知到可知,进而得到结论的应为综合法,由未知到需知,进而找到与已知的关系为分析法,故①②两条流程线与“推理与证明”中的思维方法为:①﹣综合法,②﹣分析法,故选:B.点评:本题以结构图为载体,考查了证明方法的定义,正确理解综合法和分析法的定义,是解答的关键.4.已知直角三角形的两直角边长的和为4,则此直角三角形的面积满足()A.最大值2B.最大值4C.最小值2D.最小值4考点:基本不等式在最值问题中的应用.专题:不等式的解法及应用.分析:设直角三角形的两直角边长为a,b,则a+b=4,运用基本不等式可得三角形的面积的最大值.解答:解:设直角三角形的两直角边长为a,b,则a+b=4,直角三角形的面积S=ab≤•()2=•4=2,当且仅当a=b=2,取得最大值,且为2.故选:A.点评:本题考查基本不等式的运用:求最值,考查直角三角形的面积公式及最值的求法,属于中档题.5.已知函数f(x)=,则f(f(﹣2))=()A.B.C.D.9考点:函数的值.专题:函数的性质及应用.分析:首先求出﹣2对应的函数值,然后再求其对应的函数值.解答:解:由已知,﹣2<0,所以f(﹣2)=,又>0,所以f()=;故选D.点评:本题考查了分段函数的函数值求法;关键是明确自变量所属的范围,找到对应的解析式求值.6.如图程序框图,若输入a=﹣9,则输出的结果是()2A.﹣9B.﹣3C.3D.是负数考点:选择结构.专题:图表型;算法和程序框图.分析:根据框图的流程判断a=﹣9不满足条件a≥0,执行输出是负数,从而得解.解答:解:模拟执行程序框图,可得当a=﹣9不满足条件a≥0,执行输出“是负数“.故选:D.点评:【点评】本题考查了选择结构的程序框图,根据框图的流程判断算法的功能是关键,属于基础题.7.设0<a<1,x=loga2,y=loga4,z=a2,则x、y、z的大小关系为()A.x>y>zB.y>x>zC.z>y>xD.z>x>y考点:对数值大小的比较.分析:利用对数函数和指数函数的单调性求解.解答:解: 0<a<1,∴x=loga2<loga1=0,y=loga4<loga2=x,z=a2>0,∴z>x>y.故选:D.点评:本题考查三个数大小的比较,是基础题,解题时要注意对数函数和指数函数的单调性的合理运用.8.设变量x,y满足约束条件,则目标函数z=y﹣2x的最小值为()A.﹣7B.﹣4C.1D.23考点:简单线性规划.专题:不等式的解...