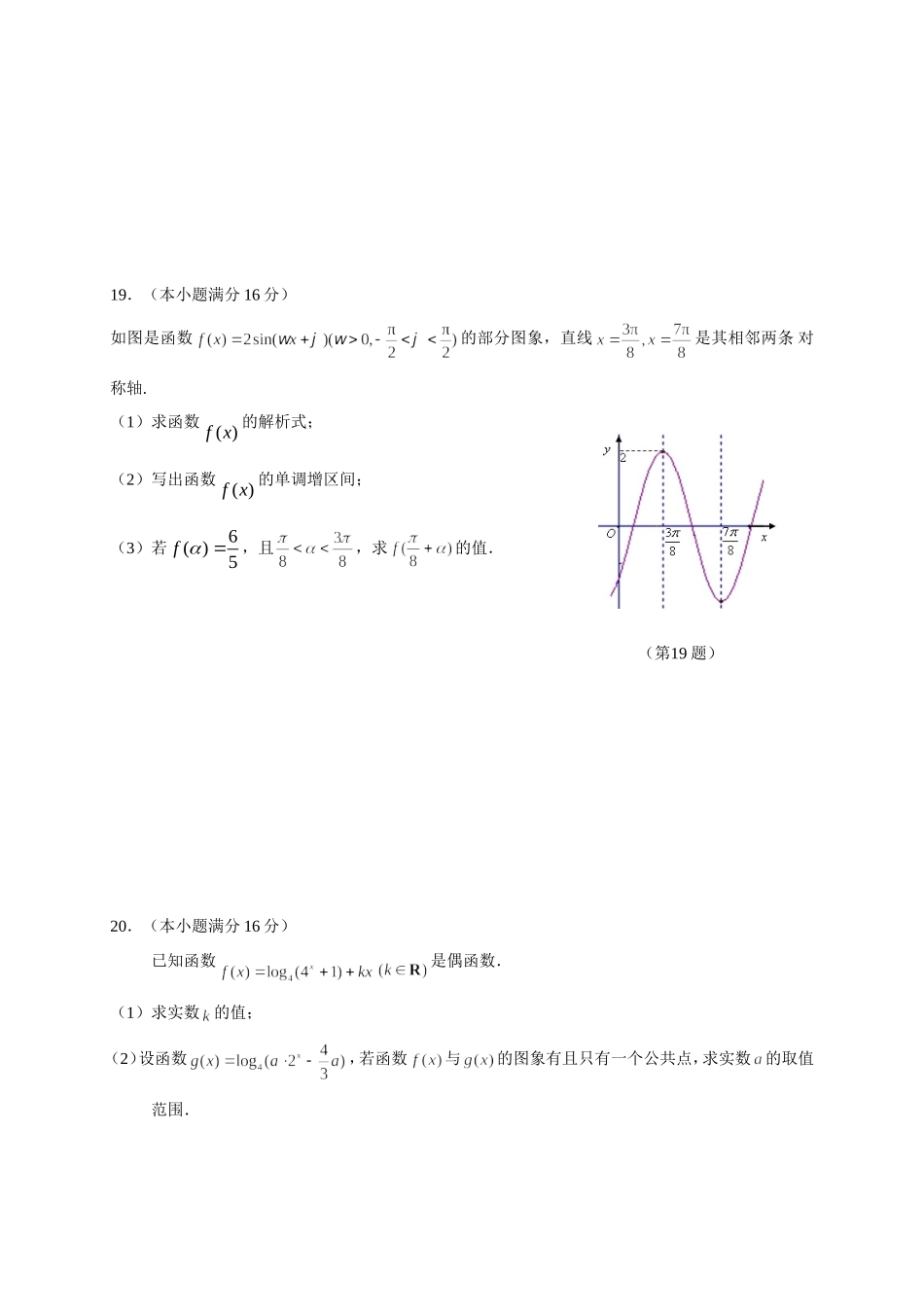
高一数学(必修1必修4)模拟练习2015年1月一、填空题:本大题共14小题,每小题5分,共70分.1.已知集合,,则.2.与角终边相同的最小正角是.(用弧度制表示)3.求值:=.4.已知点在第二象限,则角的终边在第象限.5.已知幂函数)(xfy的图象过点,则.6.设,,,则按由小到大的顺序排列为.7.已知)(xfy是定义在R上的奇函数,且当0x时,xxf21)(,则)8(log21f.8.已知则的值为.9.已知函数则满足的实数=.10.已知的单调增区间为.11.若函数的零点为,则满足的最大整数k=.12.下列说法中,所有正确说法的序号是.①终边在轴上的角的集合是;②函数在第一象限是增函数;③函数44sincosyxx的最小正周期是;④把函数的图象向右平移个单位长度得到函数3sin2yx的图象.13.若函数在区间上的值域是,则的最大值是.(第14题)14.如图,在平面直角坐标系中,过原点O的直线与函数的图象交于A,B两点,过B作y轴的垂线交函数的图象于点C,若AC平行于y轴,则点A的坐标是.二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)已知函数的定义域为集合,集合,集合.(1)求;(2)若(),求的值.16.(本小题满分14分)已知函数.(1)判断函数的奇偶性并证明;(2)当时,求函数的值域.17.(本小题满分14分)已知函数.(1)求的最小正周期和最值;(2)求这个函数的单调递增区间.18.(本小题满分16分)座落于我市金山公园内的慈寿塔具有悠久的历史.如图,若设慈寿塔AB高度为150米,某大楼CD高度为90米,从大楼CD顶部C看慈寿塔AB的张角,求慈寿塔AB与大楼CD底部之间的距离BD.ABCD45°(第18题)19.(本小题满分16分)如图是函数的部分图象,直线是其相邻两条对称轴.(1)求函数()fx的解析式;(2)写出函数()fx的单调增区间;(3)若6()5f,且,求的值.20.(本小题满分16分)已知函数是偶函数.(1)求实数的值;(2)设函数,若函数与的图象有且只有一个公共点,求实数的取值范围.(第19题)高一数学(必修1必修4)Ⅰ卷参考答案及评分标准一、填空题:本大题共14小题,每小题4分,共56分.1.2.3.4.四5.46.7.-98.9.10.11.212.③④13.14.二、解答题:本大题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤.15.解:(1)由题意得=.,=,-------------------2分∴.----------------------4分(2)由题意得=,∴,--------------6分∵,∴,--------8分∴,又∵,∴=1.--------10分16.解:(1)∵,,---------------------------4分∴是奇函数.---------------------------5分(2)令,则.-------------------------7分∵,∴,∴,∴,所以的值域是.---------------------------10分17.解:(1),最大,最小(2)18.解:如图作CEAB于E.因为AB∥CD,AB=150,CD=90,所以BE=90,AE=60.设CE=,,则.-----------2分在和中,,----------4分因为,所以.------------8分化简得,解得或(舍去).-----------10分答:慈寿宝塔AB与大楼CD底部之间的距离为180米.------------12分19.解:(1)由题意,,∴.--------1分又0,故2,∴.由,解得,又,∴,--------4分∴.---------5分(2)函数()fx的单调增区间为.---------8分(3)由题意得:,即,∵,∴,∴,---------10分,∴.---------13分20.解:(1)由题意知:任意有,即恒成立.∴恒成立,化简得对恒成立,∴.………5分(2)∵函数与的图象有且只有一个公共点,∴方程有且只有一个实根,化简得:方程有且只有一个实根,令,则方程有且只有一个正根.………7分①当时,不合题意;………8分②当时,(ⅰ)若,则.若,则不合题意;若,则合题意;………10分(ⅱ)若即时,由题意,方程有一个正根与一个负根,即,解得,∴.……12分综上所述,实数的取值范围是.……13分