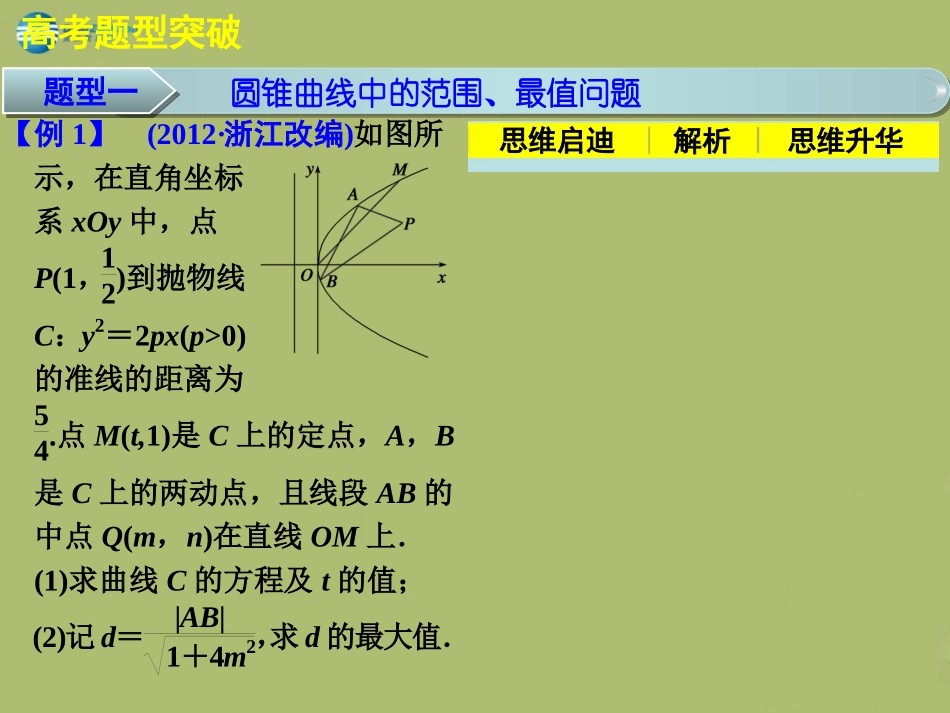
数学RB(理)第九章平面解析几何专题五高考中的圆锥曲线问题专题五高考中的圆锥曲线问题题号答案解析12345CB8BB自我检测查缺补漏考点自测题型一圆锥曲线中的范围、最值问题【例1】(2012·浙江改编)如图所示,在直角坐标系xOy中,点P(1,12)到抛物线C:y2=2px(p>0)的准线的距离为54.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB的中点Q(m,n)在直线OM上.(1)求曲线C的方程及t的值;(2)记d=|AB|1+4m2,求d的最大值.思维启迪思维升华解析高考题型突破【例1】(2012·浙江改编)如图所示,在直角坐标系xOy中,点P(1,12)到抛物线C:y2=2px(p>0)的准线的距离为54.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB的中点Q(m,n)在直线OM上.(1)求曲线C的方程及t的值;(2)记d=|AB|1+4m2,求d的最大值.(1)依条件,构建关于p,t的方程;高考题型突破思维启迪思维升华解析(2)建立直线AB的斜率k与线段AB中点坐标间的关系,并表示弦AB的长度,运用函数的性质或均值不等式求d的最大值.题型一圆锥曲线中的范围、最值问题【例1】(2012·浙江改编)如图所示,在直角坐标系xOy中,点P(1,12)到抛物线C:y2=2px(p>0)的准线的距离为54.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB的中点Q(m,n)在直线OM上.(1)求曲线C的方程及t的值;(2)记d=|AB|1+4m2,求d的最大值.解(1)y2=2px(p>0)的准线x=-p2,∴1-(-p2)=54,p=12,高考题型突破思维启迪思维升华解析∴抛物线C的方程为y2=x.又点M(t,1)在曲线C上,∴t=1.(2)由(1)知,点M(1,1),从而n=m,即点Q(m,m),依题意,直线AB的斜率存在,且不为0,设直线AB的斜率为k(k≠0).题型一圆锥曲线中的范围、最值问题【例1】(2012·浙江改编)如图所示,在直角坐标系xOy中,点P(1,12)到抛物线C:y2=2px(p>0)的准线的距离为54.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB的中点Q(m,n)在直线OM上.(1)求曲线C的方程及t的值;(2)记d=|AB|1+4m2,求d的最大值.且A(x1,y1),B(x2.y2),由y21=x1,y22=x2,得(y1-y2)(y1+y2)=x1-x2,故k·2m=1,高考题型突破思维启迪思维升华解析所以直线AB的方程为y-m=12m(x-m),即x-2my+2m2-m=0.由x-2my+2m2-m=0,y2=x消去x,整理得y2-2my+2m2-m=0,题型一圆锥曲线中的范围、最值问题【例1】(2012·浙江改编)如图所示,在直角坐标系xOy中,点P(1,12)到抛物线C:y2=2px(p>0)的准线的距离为54.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB的中点Q(m,n)在直线OM上.(1)求曲线C的方程及t的值;(2)记d=|AB|1+4m2,求d的最大值.所以Δ=4m-4m2>0,y1+y2=2m,y1y2=2m2-m.从而|AB|=1+1k2·|y1-y2|=1+4m2·4m-4m2=21+4m2m-m2高考题型突破思维启迪思维升华解析∴d=|AB|1+4m2=2m1-m≤m+(1-m)=1,题型一圆锥曲线中的范围、最值问题【例1】(2012·浙江改编)如图所示,在直角坐标系xOy中,点P(1,12)到抛物线C:y2=2px(p>0)的准线的距离为54.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB的中点Q(m,n)在直线OM上.(1)求曲线C的方程及t的值;(2)记d=|AB|1+4m2,求d的最大值.当且仅当m=1-m,即m=12时,上式等号成立,高考题型突破思维启迪思维升华解析题型一圆锥曲线中的范围、最值问题又m=12满足Δ=4m-4m2>0.∴d的最大值为1.【例1】(2012·浙江改编)如图所示,在直角坐标系xOy中,点P(1,12)到抛物线C:y2=2px(p>0)的准线的距离为54.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB的中点Q(m,n)在直线OM上.(1)求曲线C的方程及t的值;(2)记d=|AB|1+4m2,求d的最大值.圆锥曲线中的最值问题解决方法一般分两种:一是几何法,特别是用圆锥曲线的定义和平面几何的有关结论来求最值;二是代数法,常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题,然后利用均值不等式、函数的单调性或三角函数的有界性等求最值.高考题型突破思维启迪思维升华解析题型一圆锥曲线中的范围、最值问题跟踪训练1已知点A(-1,0),B(1,0),动点M的轨迹曲线C满足∠AMB=2θ,|AM→|·|BM→|cos2θ=3,过...