江苏地区数学科空间的角资料 课件VIP免费

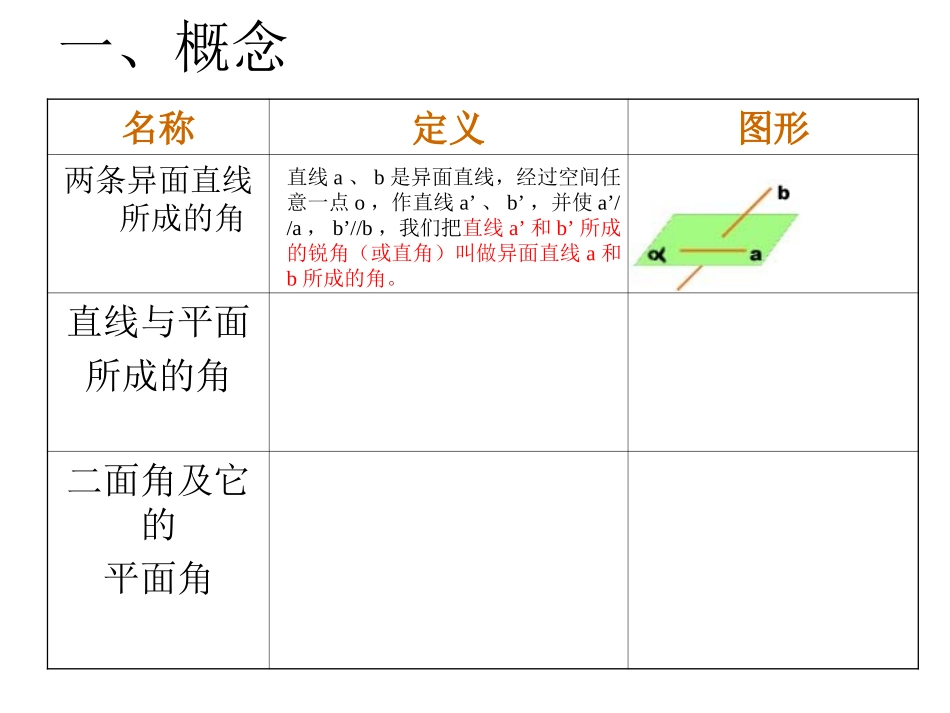
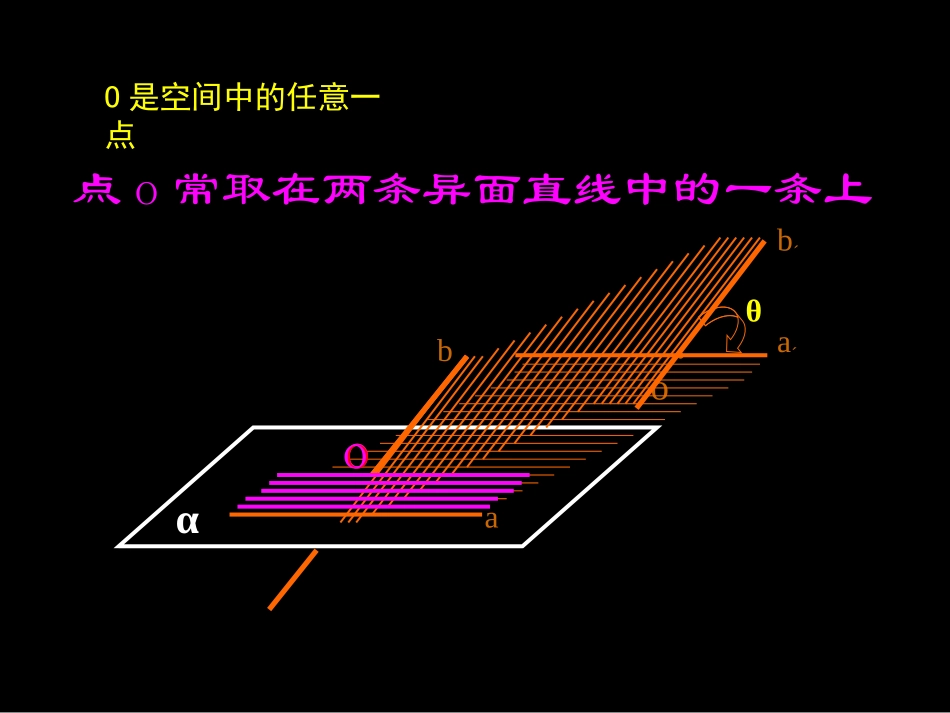
一、概念名称定义图形两条异面直线所成的角直线与平面所成的角二面角及它的平面角直线a、b是异面直线，经过空间任意一点o，作直线a’、b’，并使a’//a，b’//b，我们把直线a’和b’所成的锐角（或直角）叫做异面直线a和b所成的角。aαbo.aˊO是空间中的任意一点点o常取在两条异面直线中的一条上bˊθoooo一、概念名称定义图形两条异面直线所成的角直线与平面所成的角二面角及它的平面角直线a、b是异面直线，经过空间任意一点o，作直线a’、b’，并使a’//a，b’//b，我们把直线a’和b’所成的锐角（或直角）叫做异面直线a和b所成的角。平面的一条斜线和它在这个平面内的射影所成的锐角，叫做这条直线和这个平面所成的角，特别地，若Lᅩα则L与α所成的角是直角，若L//α或Lα，则L与α所成的角是0º的角。oLθαBA一、概念名称定义图形两条异面直线所成的角直线与平面所成的角二面角及它的平面角直线a、b是异面直线，经过空间任意一点o，作直线a’、b’，并使a’//a，b’//b，我们把直线a’和b’所成的锐角（或直角）叫做异面直线a和b所成的角。从一条直线出发的两个半平面所组成的图形叫做二面角。以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。LαθoBA平面的一条斜线和它在这个平面内的射影所成的锐角，叫做这条直线和这个平面所成的角，特别地，若Lᅩα则L与α所成的角是直角，若L//α或Lα，则L与α所成的角是的角。AαβLBO一、概念名称定义图形两条异面直线所成的角直线与平面所成的角二面角及它的平面角直线a、b是异面直线，经过空间任意一点o，作直线a’、b’，并使a’//a，b’//b，我们把直线a’和b’所成的锐角（或直角）叫做异面直线a和b所成的角。从一条直线出发的两个半平面所组成的图形叫做二面角。以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。LαθoBAAαβLBO平面的一条斜线和它在这个平面内的射影所成的锐角，叫做这条直线和这个平面所成的角，特别地，若Lᅩα则L与α所成的角是直角，若L//α或Lα，则L与α所成的角是的角。二、数学思想、方法、步骤：解决空间角的问题涉及的数学思想主要是化归与转化，即把空间的角转化为平面的角，进而转化为三角形的内角，然后通过解三角形求得。2.方法：3.步骤：b.求直线与平面所成的角：a.求异面直线所成的角：c.求二面角的大小：①作（找）②证③点④算1.数学思想：平移构造可解三角形找（或作）射影构造可解三角形找（或作）其平面角构造可解三角形A1ABB1CDC1D1FEG解：如图，取AB的中点G，O（证）A1D1FGAD又ADA1D1FG四边形A1GFD1为平行四边形A1GD1FA1G与AE所成的锐角（或直角）就是AE与D1F所成的角。（点）（算）FG，A1G，A1G与AE交于O连结（作）三、例题例1：如图，在正方体ABCD-A1B1C1D1中，E、F分别是BB1、CD中点。求AE与D1F所成的角。即直线AE与D1F所成的角为直角。E是BB1的中点tRA1AGABEAOG=90GA1A=GAO例2.已知，在矩形ABCD中，AB=4，BC=3，E为DC边上的中点，沿AE折成60º的二面角，分别求DE、DC与平面AC所成的角。ABDE34C34DEABC2二面角D—AE—B为60º解：如图（1），作DMAE⊥于M，延长DM交CB于N，ABCD2234MEMDEACBNDDDDDFN图（1）图（2）过D作DF⊥平面ABCE,连结EF、DC、CF.沿AE折成60º的二面角后如图（2）于是∠DEF是DE与平面ABCE所成的角，∠DCF是DC与平面ABCE所成的角.ABCD2234MEN图（1）EACBMNF图（2）D DMAE⊥，MN⊥AE∴DMN=60∠º，且AE⊥平面DMN又 AE⊂平面ABCE∴平面DMN⊥平面ABCE,从而垂足F在MN上.F如图（1）在Rt△ADE中，DM=136322322AEDEADME=)13413365213364134222DMDEMEAEDE（或在Rt∆DFM中，1332113660COSDMMF∴∠DEF=26135arccos即DE与平面AC所成的角为26135arccosABCD2234MENEACBMNF图（2）D图（1）在Rt∆EFM中，13522MFMEEF2613513252135DEEF在Rt∆DFE中，CosDEF=∠F在图（1）中，设∠EDM=α，在Rt∆DME中，133cosDEDM DF=DM+MF=139133136在∆DFC中，由余弦定理得：CF²=DF²+DC²-2DF·DC·Cos...