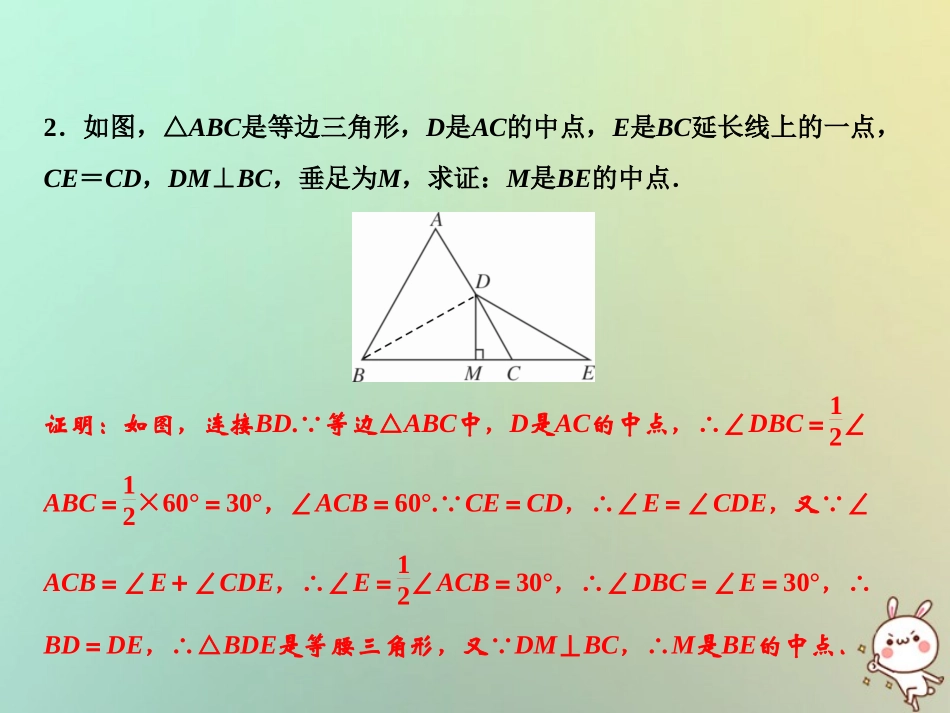
第15章轴对称图形与等腰三角形专题强化七作等腰三角形中辅助线的几种思路2018秋季数学八年级上册•HK强化角度1已知等腰作“三线”中的一线1.如图,在△ABC中,AB=AC,AE⊥BE于点E,且BE=12BC,若∠EAB=20°,则∠BAC=.40°2.如图,△ABC是等边三角形,D是AC的中点,E是BC延长线上的一点,CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点.证明:如图,连接BD.∵等边△ABC中,D是AC的中点,∴∠DBC=12∠ABC=12×60°=30°,∠ACB=60°.∵CE=CD,∴∠E=∠CDE,又∵∠ACB=∠E+∠CDE,∴∠E=12∠ACB=30°,∴∠DBC=∠E=30°,∴BD=DE,∴△BDE是等腰三角形,又∵DM⊥BC,∴M是BE的中点.3.如图,在△ABC中,AB=AC,E在CA的延长线上,∠E=∠AFE.求证:EF⊥BC.证明:如图,过点A作AD⊥BC于D.∵AB=AC,∴∠BAC=2∠1.∵∠BAC是△AEF的外角,∠E=∠AFE,∴∠BAC=2∠E,∴∠1=∠E,∴EF∥AD,∴EF⊥BC.强化角度2构造等腰三角形4.如图,△ABC的面积为1cm2,AP垂直∠ABC的平分线BP于P,则△PBC的面积为()BA.0.4cm2B.0.5cm2C.0.6cm2D.0.7cm25.如图,在△ABC中,AB=AC,点P从点B出发沿线段BA移动,同时,点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.(1)如图①,当点P为AB的中点时,求证:PD=QD;(2)如图②,过点P作直线BC的垂线,垂足为E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段?请说明理由.(1)证明:如图①,过P点作PF∥AC交BC于F.∵点P和点Q同时出发且速度相同,∴BP=CQ.∵PF∥AQ,∴∠PFB=∠ACB,∠DPF=∠DQC.又∵AB=AC,∴∠B=∠ACB,∴∠B=∠PFB,∴BP=PF,∴PF=QC.在△PFD和△QCD中,∠DPF=∠DQC∠PDF=∠QDCPF=QC,∴△PFD≌△QCD(AAS),∴PD=QD;(2)解:存在,DE的长度保持不变.理由如下:如图②,过点P作PF∥AC交BC于F.由(1)可知PB=PF.∵PE⊥BF,∴BE=EF.由(1)可知△PFD≌△QCD,∴FD=CD,∴DE=EF+FD=BE+DC=12BC,∴DE的长为定值.强化角度3利用等腰三角形构造全等6.如图,△ABC是等边三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以点D为顶点作一个60°的角,角的两边分别交AB、AC边于M、N两点,连接MN.求证:MN=BM+NC.证明:如图,延长MB到E,使BE=CN,连接DE.∵BD=CD,∠BDC=120°,∴∠1=∠2=30°.∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∴∠ABD=∠ACD=90°,∴∠DBE=90°,∴∠DBE=∠DCN.在△BDE和△CDN中,BE=CN∠DBE=∠DCNBD=CD,∴△BDE≌△CDN(SAS),∴∠3=∠4,DE=DN.∵∠BDC=120°,∠MDN=60°,∴∠4+∠BDM=60°,∴∠3+∠BDM=60°,即∠MDE=60°,∴∠MDE=∠MDN.在△MDE和△MDN中,DE=DN∠MDE=∠MDNMD=MD,∴△MDE≌△MDN(SAS),∴ME=MN.∵ME=MB+BE=MB+CN,∴MN=BM+CN.