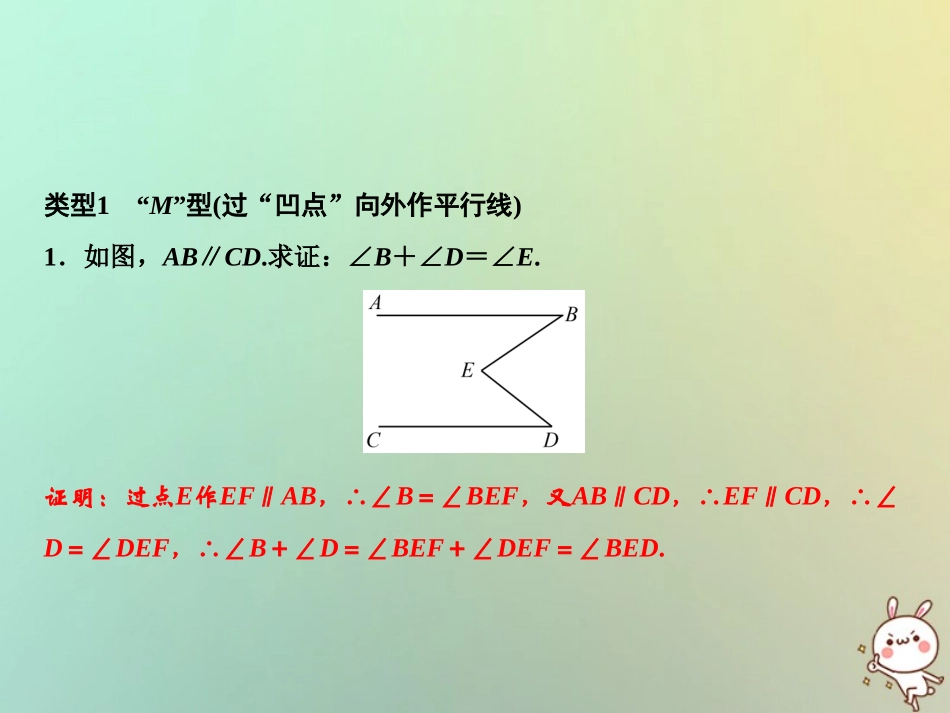
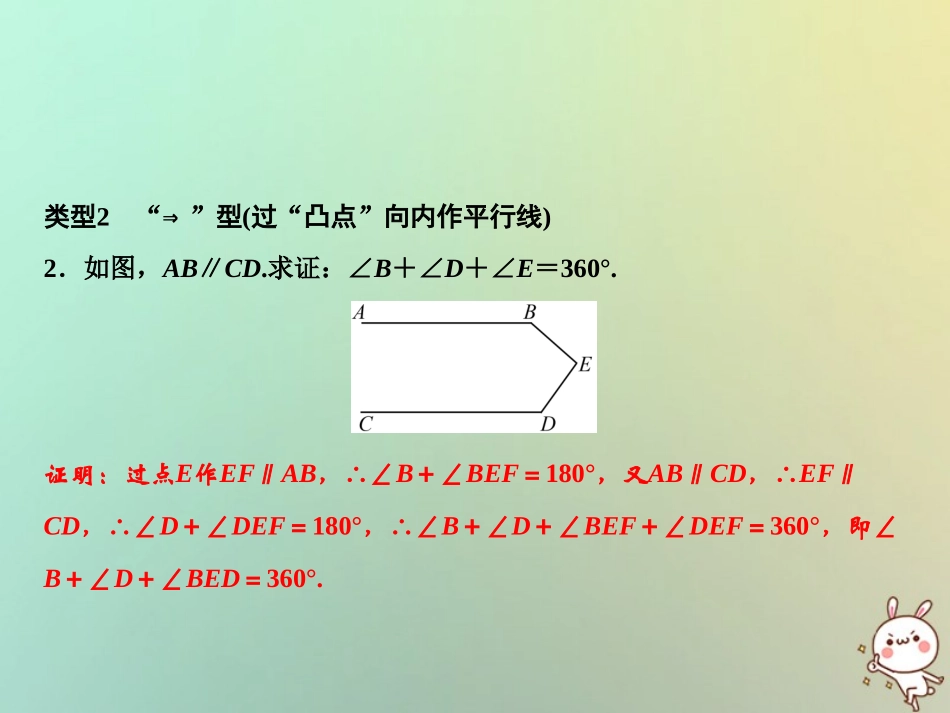
第七章平行线的证明专题突破六平行线中常见的辅助线2018秋季数学八年级上册•B类型1“M”型(过“凹点”向外作平行线)1.如图,AB∥CD.求证:∠B+∠D=∠E.证明:过点E作EF∥AB,∴∠B=∠BEF,又AB∥CD,∴EF∥CD,∴∠D=∠DEF,∴∠B+∠D=∠BEF+∠DEF=∠BED.类型2“⇒”型(过“凸点”向内作平行线)2.如图,AB∥CD.求证:∠B+∠D+∠E=360°.证明:过点E作EF∥AB,∴∠B+∠BEF=180°,又AB∥CD,∴EF∥CD,∴∠D+∠DEF=180°,∴∠B+∠D+∠BEF+∠DEF=360°,即∠B+∠D+∠BED=360°.类型3“之”字型(作多条平行线)3.如图,AB∥EF,∠BCD=90°,求x+y-z的值.解:过点C、D分别作CM、DN平行于AB、EF,∵AB∥EF,∴AB∥CM∥DN∥EF.则x=∠BCM,∠DCM=∠CDN,∠E=∠NDE,又∠NDE+∠NDC=y,∠DCM+∠BCM=90°,即x+∠MCD=90°.又∠MCD=∠NDC=y-∠NDE=y-z,∴x+y-z=90°.类型4变式运用4.(恩施中考)如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,求∠BCD的值.解:过点C作CF∥AB,∵AB∥DE,∴AB∥DE∥CF,∵∠ABC=70°,∠CDE=140°,∴∠BCF=70°,∠DCF=40°,∴∠BCD=30°.5.如图,AB∥CD,AF、CF分别为∠BAE、∠DCE的平分线,求∠E、∠F之间的数量关系.解:∠E=2∠F.过点E作EG∥AB,∵AB∥CD,∴EG∥CD.∴∠AEG=∠BAE,∠CEG=∠DCE.∴∠AEC=∠BAE+∠DCE.作FH∥AB,则FH∥CD.∴∠AFH=∠BAF,∠CFH=∠DCF.∴∠AFC=∠BAF+∠DCF.∵AF、CF分别平分∠BAE、∠ECD,∴∠BAF=12∠BAE,∠DCF=12∠DCE.∴∠AFC=12(∠BAE+∠DCE)=12∠AEC.