苏教版高一数学向量的数量积 课件VIP免费

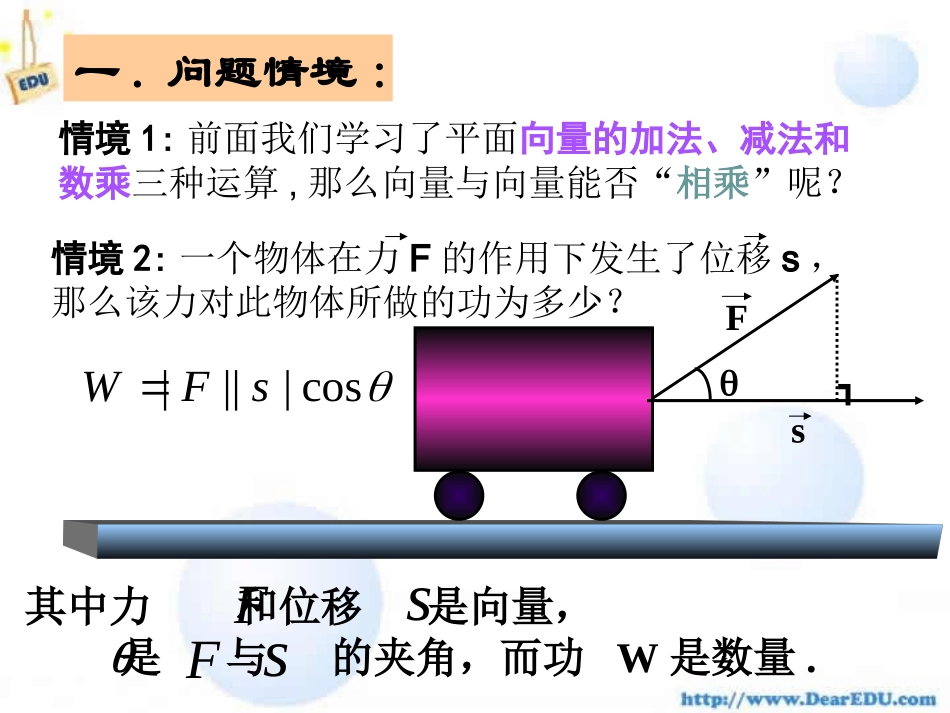
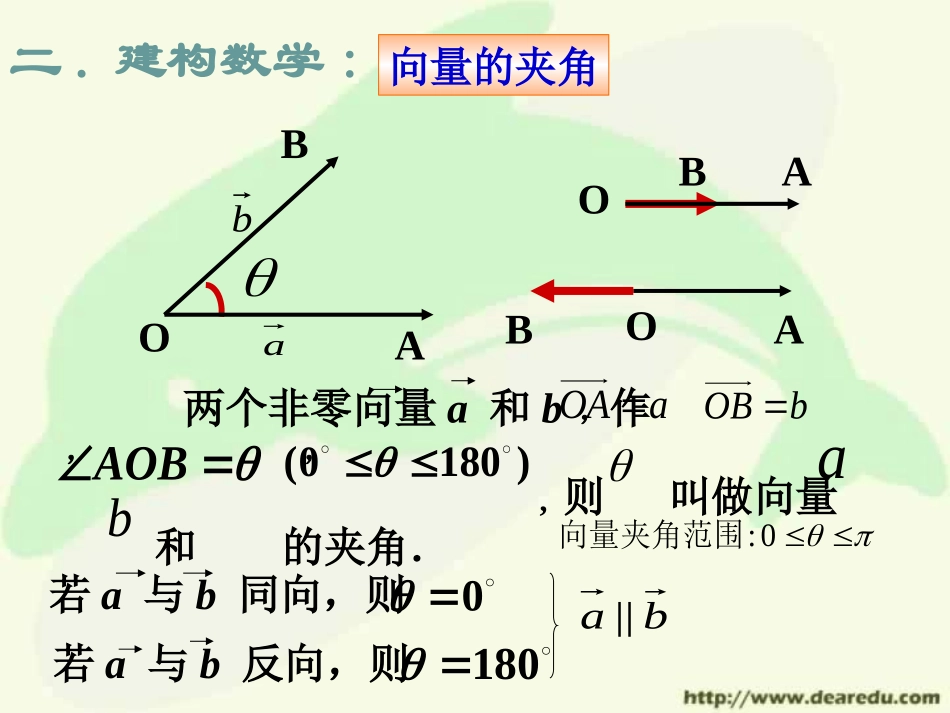
Fs┓一.问题情境:情境1:前面我们学习了平面向量的加法、减法和数乘三种运算,那么向量与向量能否“相乘”呢？cos||||sFW其中力和位移是向量，是与的夹角，而功W是数量.FssF情境2:一个物体在力F的作用下发生了位移s，那么该力对此物体所做的功为多少？Fs┓向量的夹角OABOAB若a与b反向，则180两个非零向量a和b，作，，,则叫做向量和的夹角．aOAbOBAOB)1800(ab二.建构数学:ba||OABab0:向量夹角范围若a与b同向，则0如图,等边三角形ABC中,求（1）AB与AC的夹角；（2）AB与BC的夹角。ABC通过平移变成共起点！12060'CD0120向量的数量积的定义cos||||baba已知两个非零向量a和b，它们的夹角为，我们把数量叫做a与b的数量积（或内积），记作a·b，即cos||||ba一种新的运算，请牢记！建构数学:OABba规定:0·a=0（2）两向量的数量积是一个数量,而不是向量,（1）一种新的运算。向量的数量积特点：（3）a·b不能写成a×b，a×b表示向量的另一种运算．也不能写成a·b。符号由夹角决定。cos||||baba三.探究与发现:baba,)1(同向时与当||||bababa,)2(反向时与当||||bababa,)3(时当0?||||||)4(成立吗baba||||||babacos||||baba运算律：a·a=|a|2（简写a2=|a|2）aaa||或a·c＋b·c(1)a·b=b·a(3)(a＋b)·c=(2))(bababacos||||baba(交换律)(分配律)探究与发现:?aaa与|a|的关系:(性质)已知均为非零向量,试判断下列说法是否正确:cba,,00)1(a(×)(×)00)2(abababa|||,|||)3(则若(√)22||)4(aaaa(√).0,0)5(中至少有一个为与则若baba(×)四.应用数学:*.已知△ABC中,AB=a,AC=b,当a·b<0,a·b=0时,ABC△各是什么三角形？当a·b＜0时，cos<0，为钝角三角形当a·b=0时，为直角三角形当a·b＜0时，cos<0，为钝角三角形cos||||baba例.|a|=2，|b|=5，a与b的夹角为600，求：(2)(a+2b)·(a-3b)(3)(a+b)2(4)|a+b|应用数学:ba)1(ba:解060cos||||ba52152baba22||6||:原式分析原式分析:baba2||||22分析:.,)(2再开方先求baa·a=|a|2（简写a2=|a|2）aaa||或性质2222)(bbaaba22)()(bababa（1）（2）探究:下列等式成立吗?baba2||||2222||||ba夹角的范围运算律性质数量积0(3)(a＋b)·c=a·c＋b·ca·a=|a|2（简写a2=|a|2）aaa||或五.知识回顾:cos||||baba(2))(bababa(1)a·b=b·a(交换律)(分配律)六.作业:P.80.2;P.82.2(习题).)())(2(;,)1(cbacbacbcaba则课后思考:向量的数量积运算是否满足消去律和结合律?即:是否成立?