高一数学 知识结构总复习课件 苏教版必修1 课件VIP免费

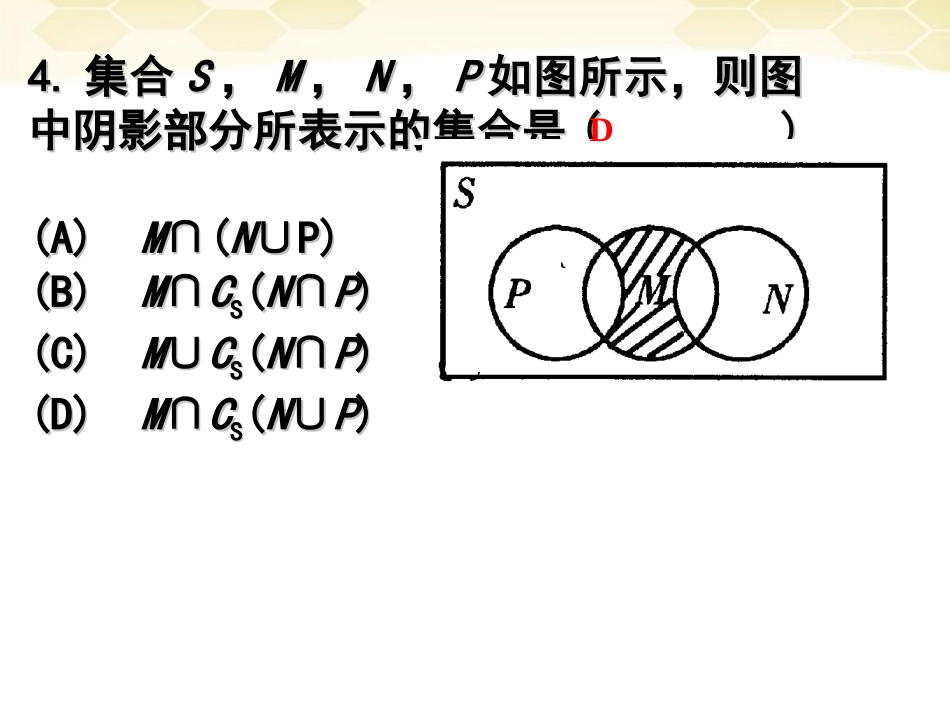
集合集合含义与表示集合间关系集合基本运算列举法描述法图示法子集真子集补集并集交集一、知识结构211-，，M2.2.已知集合集合已知集合集合则则MM∩∩NN是是()()421，，AB{1}C{1AB{1}C{1，，2}DΦ2}DΦ，，MxxyyN2二、例题与练习1.1.集合集合A={1,0,x},A={1,0,x},且且xx22∈A,∈A,则则xx＝＝。。3.3.满足满足{1,2}A{1,2,3,4}{1,2}A{1,2,3,4}的集合的集合AA的个的个数有数有个个-1-1BB33变式：xyxNRxyyMx3log1|,,2|4.4.集合集合SS，，MM，，NN，，PP如图所示，则图如图所示，则图中阴影部分所表示的集合是中阴影部分所表示的集合是()()(A)(A)MM∩(∩(NN∪P)∪P)(B)(B)MM∩∩CCSS((NN∩∩PP))(C)(C)MM∪∪CCSS((NN∩∩PP))(D)(D)MM∩∩CCSS((NN∪∪PP))D5.设,其中,如果，求实数a的取值范围222{40},{2(1)10}AxxxBxxaxaxRABB新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆6.设全集为R，集合，（1）求：A∪B，CR(A∩B)；（2）若集合,满足，求实数a的取值范围。}31|{xxA}242|{xxxB}02|{axxCCCB7.设,且，求实数的a取值范围。BCCAxxyyBaxxA,103|,3|AxxzzC,5|知识结构概念三要素图象性质指数函数应用大小比较方程解的个数不等式的解实际应用对数函数函数函数定义域奇偶性图象值域单调性二次函数指数函数对数函数函数的复习主要抓住两条主线1、函数的概念及其有关性质。2、几种初等函数的具体性质。反比例函数函数的概念函数的概念BCx1x2x3x4x5y1y2y3y4y5y6A函数的三要素：定义域，值域，对应法则A.B是两个非空的集合,如果按照某种对应法则f，对于集合A中的每一个元素x，在集合B中都有唯一的元素y和它对应，这样的对应叫做从A到B的一个函数。反比例函数反比例函数kyx1、定义域.2、值域3、图象k>0k<0(,0）（0，+）(,0）（0，+）二次函数二次函数yaxbxc21、定义域.2、值域3、图象a>0a<0[,)442acba(,]442acba.R指数函数指数函数1、定义域.2、值域.R3、图象a>100,a1)对数函数对数函数yxaalog其中且a>011、定义域.2、值域R3、图象a>10f(x2),那么就说f(x)在这个区间上是减函数。反比例函数反比例函数kyx1、定义域.2、值域4、图象k>0k<0(,0）（0，+）(,0）（0，+）(,0)()递减，0，+3、单调性(,0)()递增，0，+二次函数二次函数yaxbxc21、定义域.2、值域.R3、单调性4、图象a>0a<0[,)442acba(,]...