高三数学三角函数-解三角形课件VIP免费

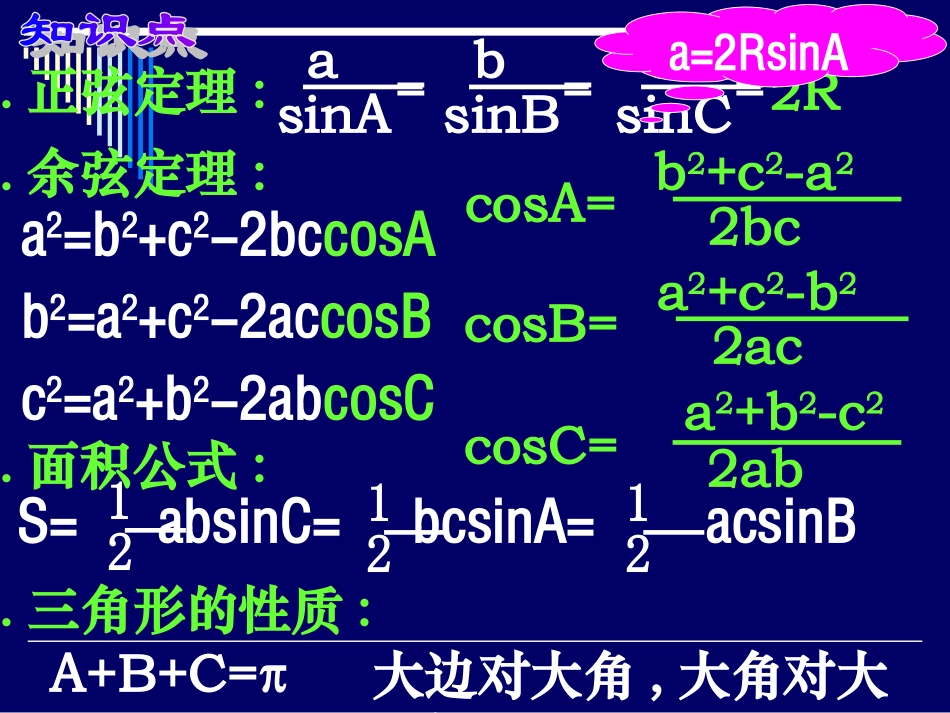
1.正弦定理:asinA=bsinB=csinC=2R2.余弦定理:a2=b2+c2-2bccosAb2=a2+c2-2accosBc2=a2+b2-2abcosCcosA=b2+c2-a22bccosB=a2+c2-b22accosC=a2+b2-c22ab3.面积公式:S=12absinC=12bcsinA=12acsinB4.三角形的性质:A+B+C=π大边对大角,大角对大边a=2RsinA2.△ABC中,“A>B”是“sinA>sinB”的条件.1.△ABC中,sinA:sinB:sinC=3:2:4,则cosC=.A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件41C1.应用正、余弦定理解三角形:①已知三边,求其它;②已知两边及其夹角,求其它;③已知两边及一边对角,求其它;④已知一边及两角,求其它;用余弦定理用余弦定理正弦定理、余弦定理都可以用正弦定理(1)求BC的长;,1055sinC△ABC中,B=450,AC=(2)设AB中点为D,求中线CD的长.ABCD10求角A,B,C.△ABC中,角A,B,C所对的边分别为a,b,c,acbAA3,45cos)2(cos2若1.△ABC中,,45,2,30Bba求∠A;2.四边形ABCD中,AD⊥CD,AD=10,AB=14,∠BDA=600,∠BCD=1350,求BD及BC的长。ABCD10146003.△ABC中,321,222bcbcacb且求∠A及tanB的值.1.ABC△中,若,coscos)3(CaAcb则cosA=A.等腰三角形B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形2.ABC△中,若a·cosA=b·cosB,则△ABC的形状是（）3.ABC△中,A=2B,则ba的取值范围是：33C（1,2）1.会用正余弦定理,结合三角形的性质解三角形,求解时注意解的情况;2.会用正余弦定理进行边角互化,关键是统一.已知两边及一边对角,求其它.会有二解,一解的情况.