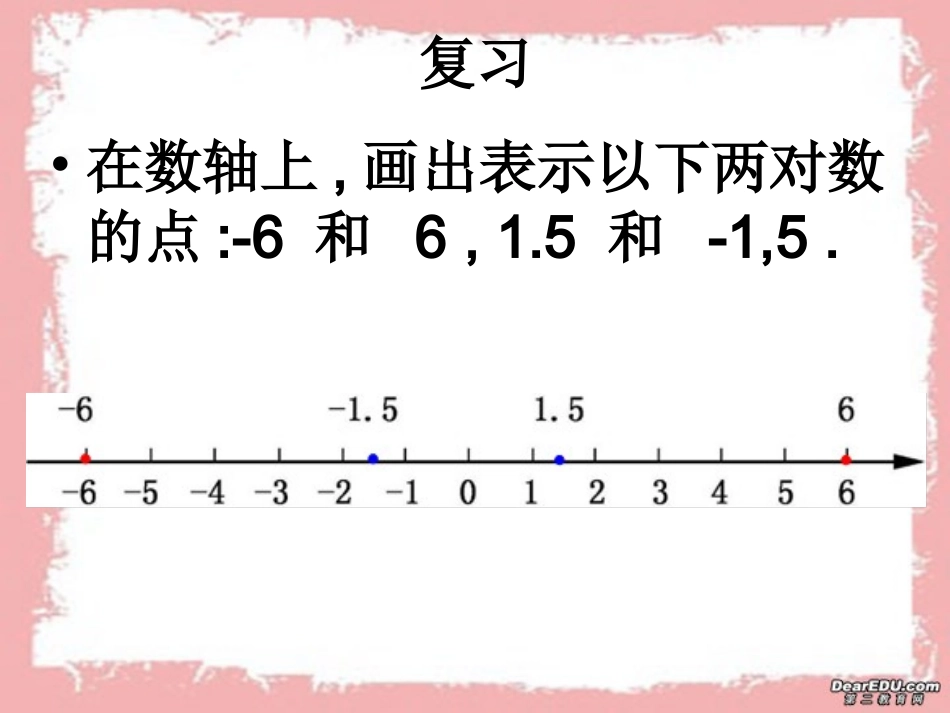
第5课时1.2.3相反数复习•在数轴上,画出表示以下两对数的点:-6和6,1.5和-1,5.想一想在数轴上,表示每对数的点有什么相同?•在数轴上,-6和6位于原点两旁,且与原点的距离相等,也就是说,它们相对于原点的位置距离相同只有方向不同.1.5和-1.5也是这样.象这样只有符号不同的两个数叫做互为相反数(oppositenumber)•如9和-9互为相反数.即9是-9的相反数.-9是9的相反数.•再如2的相反数是-2,-2的相反数是2;5的相反数是-5,-5的相反数是5.一般地,a和互为相反数,特别地,0的相反数仍是0.思考:数轴上表示相反数的两个点和原点有什么关系?•在数轴上表示互为相反数的两数的点分别位于原点的两旁,且与原点的距离相等.例1分别写出下列各数的相反数:5,-7,-213,+11.2.解:5的相反数是-5.-7的相反数是7.-213的相反数是213.+11.2的相反数是-11.2.我们通常把在一个数前面添上“-”号,表示这个数的相反数.例如-(-4)=4,-(+5.5)=-5.5,-0=0.同样,在一个数前面添上“+”号,表示这个数本身.例如+(-4)=-4,+(+12)=12,+0=0.例2化简下列各数:(1)-(+10);(2)+(-0.15);(3)+(+3);(4)-(-20).•解(1)-(+10)=-10.(2)+(-0.15)=-0.15.•(3)+(+3)=+3=3.(4)-(-20)=20.课堂练习:1.填空:(1)2.5的相反数是;(2)是-100的相反数;(3)515是的相反数;(4)的相反数是-1.1;(5)8.2和互为相反数.2.化简下列各数:(1)-(+0.78);(2)+(+519);(3)-(+25);(4)-(-3.14);(5)+(-10.1);(6)-(-16);(7)+(-12);(8)+(-0);(9)+(+2.1);(10)-(+33);(11)3;(12)5.1.课堂练习:课堂练习:3.判断下列语句是否正确,为什么?(1)符号相反的两个数叫做互为相反数;(2)互为相反数的两个数不一定一个是正数,一个是负数;(3)相反数和我们以前学过的倒数是一样的.课堂练习:4.分别写出下列各数的相反数:-2.5,1,0,213,-(+10).课堂练习:5.画出数轴,在数轴上表示下列各数及它们的相反数:414,-2,0,-3.75.课堂练习:6.回答下列问题:(1)什么数的相反数大于本身?(2)什么数的相反数等于本身?(3)什么数的相反数小于本身?