高三数学一轮复习 第3章 三角函数第3课时 三角函数的图象和性质精品课件 文 北师大版 课件VIP免费

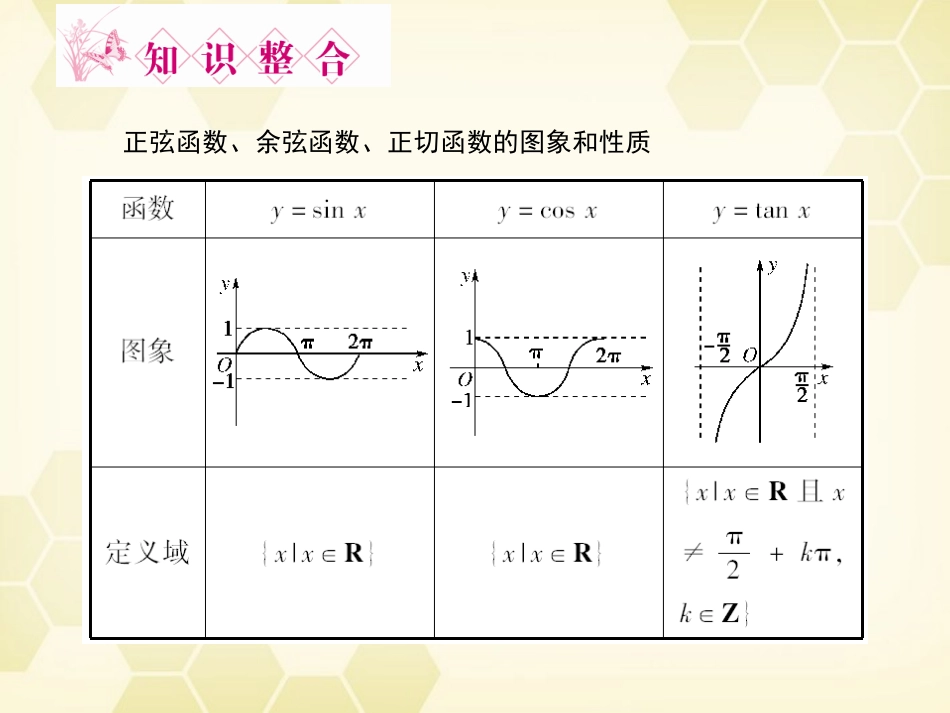
第3课时三角函数的图象和性质正弦函数、余弦函数、正切函数的图象和性质【思考探究】正弦函数和余弦函数的图象的对称轴及对称中心与函数图象的关键点有什么关系？提示：y＝sinx与y＝cosx的对称轴方程中的x都是它们取得最大值或最小值时相应的x，对称中心的横坐标都是它们的零点．1．使函数y＝1＋3cos2x(x∈R)取最大值的自变量x的集合为()A．{0}B．{x|x＝kπ，k∈Z}C．{x|x＝2kπ，k∈Z}D.x|x＝2kπ＋π2，k∈Z答案：B2．函数y＝tanπ4－x的定义域是()A.x|x≠π4，x∈RB.x|x≠－π4，x∈RC.x|x≠kπ＋π4，k∈Z，x∈RD.x|x≠kπ＋3π4，k∈Z，x∈R解析： x－π4≠kπ＋π2，∴x≠kπ＋34π，k∈Z.答案：D解析： f(x)＝2sinxcosx＝sin2x，∴f(x)为奇函数，∴f(x)的图象关于原点对称．答案：B3．(2010·陕西卷)对于函数f(x)＝2sinxcosx，下列选项中正确的是()A．f(x)在π4，π2上是递增的B．f(x)的图象关于原点对称C．f(x)的最小正周期为2πD．f(x)的最大值为24．比较大小，sin－π18________sin－π10.解析：因为y＝sinx在－π2，0上为增函数且－π18＞－π10，故sin－π18＞sin－π10.答案：＞5．函数y＝sinx＋π3，x∈0，π3的值域是________．解析： x∈0，π3，∴x＋π3∈π3，23π，∴32≤sinx＋π3≤1.答案：32，11．求三角函数的定义域，既要注意一般函数的定义域的规律，又要注意三角函数本身的特有属性，如题中出现tanx，则一定有x≠kπ＋π2(k∈Z)．2．求三角函数的定义域通常使用三角函数线、三角函数图象和数轴．(1)求函数y＝1－2cosπ2－x的定义域；(2)y＝2＋log12x＋tanx.解析：(1)由函数1－2cosπ2－x≥0，得sinx≤22，利用单位圆或三角函数的图象，易得所求函数的定义域是x2kπ－5π4≤x≤2kπ＋π4，k∈Z.(2)要使函数有意义，则2＋log12x≥0，x＞0，tanx≥0，x≠kπ＋π2，k∈Z，得0＜x≤4，kπ≤x＜kπ＋π2k∈Z.∴函数定义域是x0＜x＜π2或π≤x≤4.【变式训练】1.求下列函数的定义域：(1)y＝lgsin(cosx)；(2)y＝lg(2sinx－1)＋1－2cosx.解析：(1)要使函数有意义，必须使sin(cosx)＞0. －1≤cosx≤1，∴0＜cosx≤1.方法一：利用余弦函数的简图得知定义域为x－π2＋2kπ＜x＜π2＋2kπ，k∈Z.方法二：利用单位圆中的余弦线OM，依题意知0＜OM≤1，∴OM只能在x轴的正半轴上．∴其定义域为x－π2＋2kπ＜x＜π2＋2kπ，k∈Z.(2)要使原函数有意义，必须有：2sinx－1＞0，1－2cosx≥0，即sinx＞12，cosx≤12.由图知，原函数的定义域为：2kπ＋π3，2kπ＋5π6(k∈Z)．求解三角函数的值域(最值)的一般方法：(1)利用sinx、cosx的值域；(2)形式复杂的函数应化为y＝Asin(ωx＋φ)＋k的形式逐步分析ωx＋φ的范围，根据正弦函数单调性写出y＝Asin(ωx＋φ)的值域；(3)换元法：把sinx、cosx看作一个整体，可化为二次函数．求下列函数的值域；(1)y＝2cos2x＋2cosx；(2)y＝3cosx－3sinx；(3)y＝sinx＋cosx＋sinxcosx.解析：(1)y＝2cos2x＋2cosx＝2cosx＋122－12.当且仅当cosx＝1时，得ymax＝4，当且仅当cosx＝－12时，得ymin＝－12，故函数值域为－12，4.(2)y＝3cosx－3sinx＝2332cosx－12sinx＝23cosx＋π6. cosx＋π6≤1，∴该函数值域为－23，23.(3)y＝sinxcosx＋sinx＋cosx＝sinx＋cosx2－12＋2sinx＋π4＝sin2x＋π4＋2sinx＋π4－12＝sinx＋π4＋222－1，所以当sinx＋π4＝1时，y取最大值1＋2－12＝12＋2；当sinx＋π4＝－22时，y取最小值－1...