高一数学对数函数 苏教版 课件VIP免费

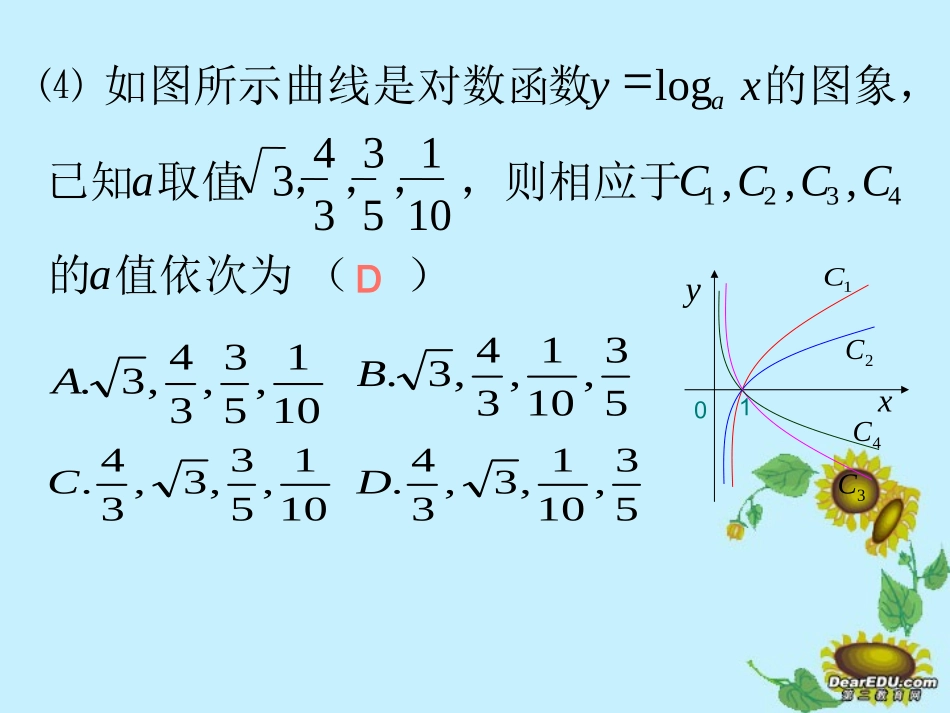
对数函数（2）㈠复习旧知：的定义域函数⑴xxy416log1.Mxyaaa过定点的图象必经时函数且当⑵1log10.由图象比较大小：⑶5log705.0log7.005.0log705log7.000,21xxx且1,1>><<101,53,34,3.A53,101,34,3.B101,53,3,34.C53,101,3,34.D1xy01C2C4C3C）（值依次为的，则相应于，，，取值已知的图象，数如图所示曲线是对数函⑷aCCCCaxya4321,,,10153343logD㈡新授：例1．7log,2log55⑴7log,2log5.05.0⑵解:,log5xy考察对数函数15上是单调增函数。，在0log5xy720又7log2log557log,2logaa⑶解:时，当10a上是减函数，在0logxya7207log2logaa时，当1a上是增函数，在0logxya7207log2logaa引申:10a1anmnm范围则⑸满足、则⑷满足、则⑶范围则⑵范围则⑴xxxnmnmnmnmaaaaaa,32log1log,loglog,loglog,7log2log,7log2log5.05.030sin30sin55.....231x合作探究:满足的关系。、求①nmnmaa,loglogxgxfaaloglog解不等式：②01nma时，当nma010时，当xgxfxgxfa0010时，当等价于:xgxfxgxfa001时，当小结:⑴同底类型比较大小,利用单调性.⑵逆向问题:xxfxxxxaaalog,loglog,2121则为函数.减⑶逆向问题:，则为增函数，21logloglogxxxxfaaa.021xx，则为减函数，21logloglogxxxxfaaa.210xx课堂练习:⑴比较大小:55.0ln56.0ln4.5log5.5log的范围则⑵aaa,5.5log4.5log<<.1a的范围则⑶aa,1log32.32a的范围则⑷xx,11log2151.01x例2.的大小。与比较5log5log72解:法一:15log,15log725log5log72中间量法法二:5log25log75log5log72图象法1xyxy2logxy7log05x法三:7log172log12555log,5log7log2log055又7log12log1555log5log72故倒数法则引申:满足、则nmnm,05log5log.10nm变式:底与真数都不同:的大小。比较3log,5log,7log7.075答案:3log5log7log7.075小结:①底不同真数同利用中间量法或函数性质.②底不同真数不同利用中间量法.例3.的大小。，试比较已知xcxbxadxddddloglogloglog,,122解:法一:dxd1,11log00,0xbad且0loglogxddxxxxbaddddlog2logloglog222又2loglogxxdd1loglog0dxddbabac0法二:1212loglog2logloglog222xxxxxbaddddd0bbabac0小结：多个数比较大小先分类（0或1为界），再作差或作商比较大小变式：的大小。，试比较已知22loglog1,1xbxadxdd练习:大小。试比较已知xxxxlglg,lg,lg,10,122分析:①定范围,分类;②作差法或作商法解:10,1x1lg0x,1,0lg2x,0,lglgx2,0lg2lg2xx2lglglg2lglglg222xxxxxx又02lgx02lglgxx22lglgxx22lglglglgxxx思考题:的大小。与比较xxaa2log2log课堂小结:一.比较大小的方法：1.同底问题------单调性法2.不同底问题-------中间量法，函数性质法3.多个数比较---------先分类再比较4.复杂问题------------作差法或作商法二.单调性的应用：比较大小，范围问题