高一数学 正余弦函数的图象 课件VIP免费

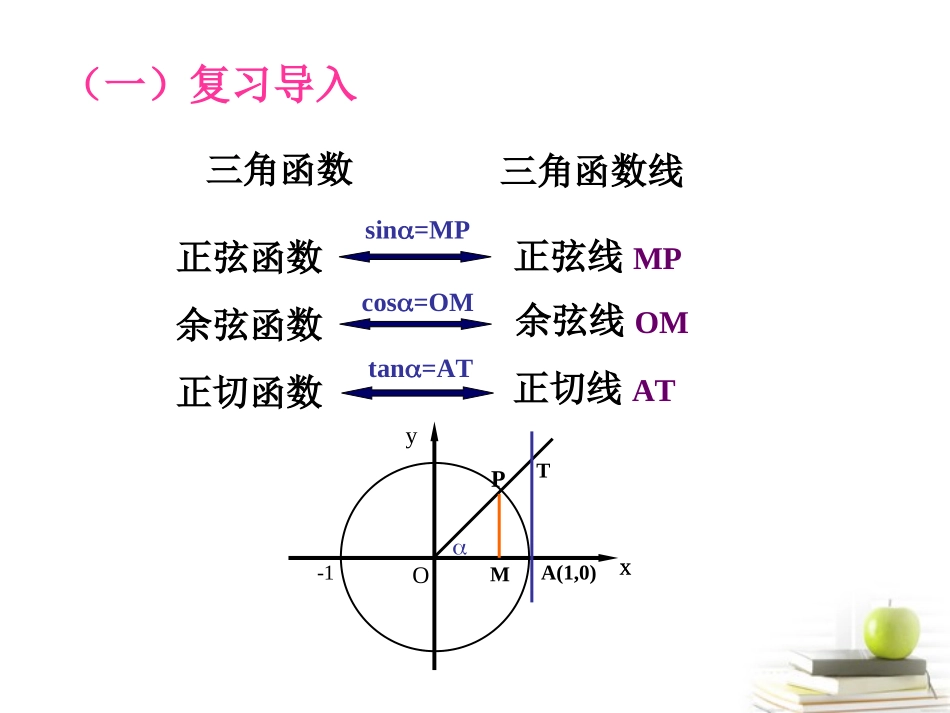
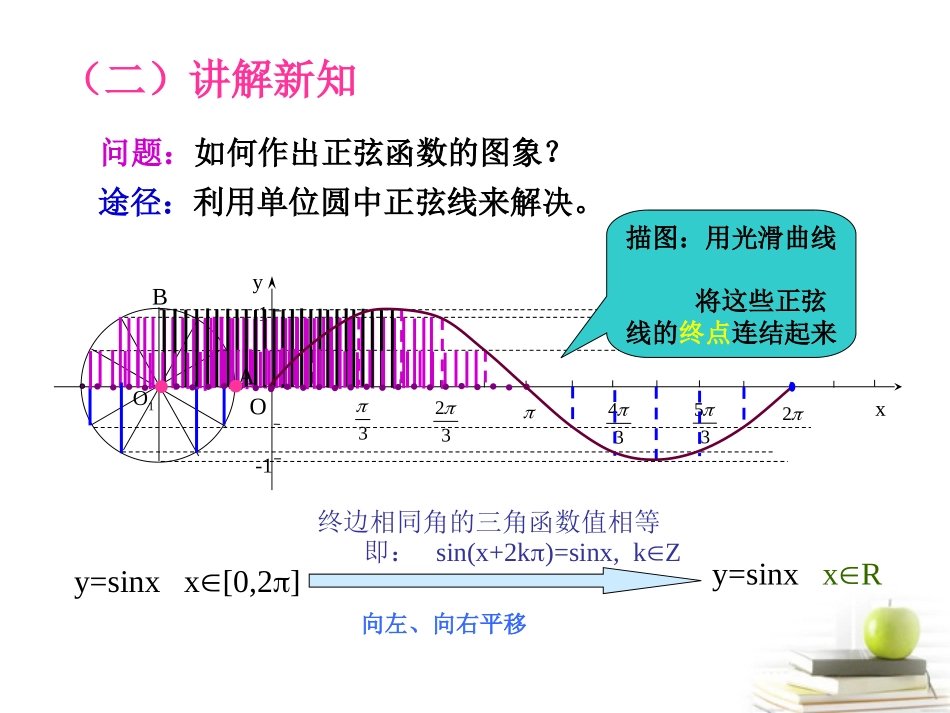
三角函数三角函数线正弦函数余弦函数正切函数正切线AT（一）复习导入yxO-1PMA(1,0)Tsin=MPcos=OMtan=AT正弦线MP余弦线OM（二）讲解新知问题：如何作出正弦函数的图象？途径：利用单位圆中正弦线来解决。y=sinxx[0,2]O1Oyx33234352-11y=sinxxR终边相同角的三角函数值相等即：sin(x+2k)=sinx,kZ描图：用光滑曲线将这些正弦线的终点连结起来向左、向右平移ABx6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正弦曲线yxo1-122322每次平移2π个单位长度x6yo--12345-2-3-41余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线正弦曲线形状完全一样只是位置不同如何画出余弦函数图像？向左平移个单位长度2正弦函数的图象yxo1-122322(0,0)(,1)2(,0)(,-1)23(2,0)五点画图法五点法——(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)yxo1-122322余弦函数的图像)1,0()0,2()1,()0,23()1,2(关键点：)1,0()0,2()1,()0,23()1,2(你能找出]2,0[,cosxxy的关键点吗？(三)例题分析例1（1）画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-101o1yx22322-12y=sinx，x[0,2]y=1+sinx，x[0,2]步骤：1.列表2.描点3.连线2101向上平移1个单位长度（2）画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1010-1yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]关于x轴对称（四）练习巩固.22320xTcos)3cos(2x332667350110120202在)3cos(2xy用五点法作函数]35,3[的图像。令3xT则Tycos2Txoy1-136326735-22的简图.)3cos(2xy用五点法作函数)2,3()0,6()2,32()0,67()2,35(（五）小结:（1）利用单位圆中正弦线作出sin,Ryxx的图象，明确图象的形状；（3）用“五点法”作出正弦函数、余弦函数的简图，并利用图象解决一些有关问题．cos,Ryxx（2）由诱导公式，作出的图象；πcossin()2xx(六)作业)42cos(2xy作出函数在区间],0[上的图像。