河北省高考数学第一轮总复习知识点检测 10.1直线与方程课件 旧人教版 课件VIP免费

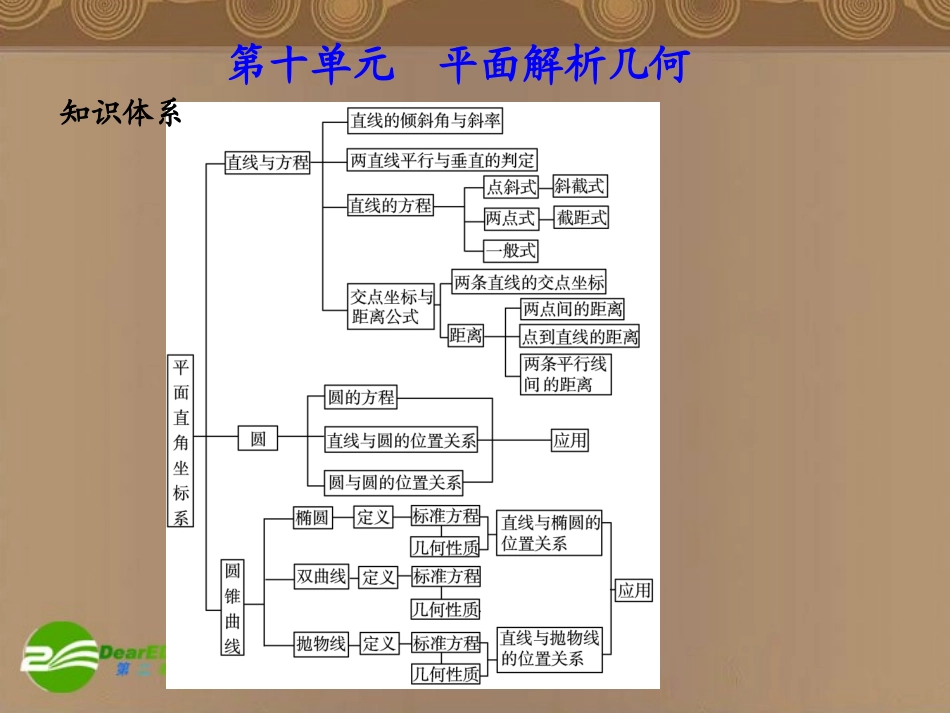
第十单元平面解析几何知识体系第一节直线与方程基础梳理1.直线的倾斜角与斜率（1）直线的倾斜角①定义：x轴正向与直线向上的方向所成的角叫做这条直线的倾斜角.②倾斜角的范围为0°≤α<180°.(2)直线的斜率①定义:把直线y=kx+b中的系数k叫做这条直线的斜率.②过两点的直线的斜率公式经过两点(其中)的直线的斜率公式为llll111222,,,PxyPxy12xx2121yykxx名称方程适用范围点斜式不含直线斜截式ｙ＝ｋｘ＋ｂ不含垂直于ｘ轴的直线两点式不含直线和直线截距式不含垂直于坐标轴和过原点的直线一般式Ａｘ＋Ｂｙ＋Ｃ＝０平面直角坐标系内的直线都适用2.直线方程的五种形式00yykxx112121yyxxyyxx1xyab0xx112xxxx112yyyy220AB典例分析题型一直线的倾斜角和斜率【例1】直线xcosα+y+2=0的倾斜角的范围是()A.B.C.D.35,(,]622650,[,)6650,65,66分析先求斜率的取值范围，再求倾斜角的取值范围.解由直线xcosα+y+2=0,所以直线的斜率为k=设直线的倾斜角为β,则tanβ=3cos3cos3又即所以β∈.3cos3,33333tan3350,[,)66学后反思求倾斜角范围的步骤是：（1）求出斜率的取值范围；（2）利用正切函数的单调性，结合图象，确定倾斜角的取值范围.举一反三1.直线xcosθ+y-1=0(θ∈R)的倾斜角的范围是()A.[0,π)BC.D3,44,4430,[,)44解析设倾斜角为α,则k=tanα=-cosθ. θ∈R,-1≤-cosθ≤1,∴-1≤tanα≤1，∴α∈.30,[,)44答案D题型二求直线的方程【例2】求下列直线的方程.（1）过点A(0,2),它的倾斜角的正弦是;(2)过点A(2,1),它的倾斜角是直线：3x+4y+10=0的倾斜角的一半.l351l分析由已知条件求出直线的斜率，然后用适当形式写出直线的方程.解（1）设直线的倾斜角为α,则sinα=，所以tanα=±,故的方程为y=±x+2，即3x-4y+8=0或3x+4y-8=0.(2)设直线和的倾斜角分别为α、β，则,又tanβ=-,故-=tan2α=，解得tanα=3或tanα=-(舍去).由点斜式，得y-1=3(x-2),即3x-y-5=0.l3534l34l1l2343422tan1tan13学后反思求直线方程首先要根据已知条件选择合适的方程形式，同时注意各种形式的适用条件.用斜截式或点斜式时，直线的斜率必须存在，而两点式不能表示与坐标轴垂直的直线，截距式不能表示与坐标轴垂直或经过原点的直线等.举一反三l2.直线过点(-3,4),且在两坐标轴上的截距之和为12,求直线的方程.l解析由于直线在两坐标轴上的截距之和为12，因此直线在两轴上的截距都存在且不过原点，故可设为截距式直线方程.设直线的方程为,则a+b=12.①又直线过点(-3,4),则.②a=9,a=-4,由①、②解得或b=3b=16.故所求的直线方程为或,即x+3y-9=0或4x-y+16=0.ll1xyabl341ab193xy1416xy题型三与直线方程有关的最值问题【例3】直线过点M(2,1),且分别与x、y轴交于A、B两点，O为原点.求当△AOB面积最小时，直线的方程.ll分析先根据题意，用点斜式设出直线的方程，然后求方程中的参数，从而求出直线的方程.解方法一：如图所示，直线如果通过一、二、三或一、三、四象限时，△AOB的面积不存在最值，因此只考虑直线与x,y轴正方向相交的情况，这时斜率必为负值.设直线的方程为y-1=k(x-2)（k＜0）,lll则有A(2-,0)与B(0,1-2k)，所以当且仅当,即k=-时，等号成立.故直线的方程为y-1=-(x-2),即x+2y-4=0.1k11111()12244444222Skkkkk14kk12l12方法二：设过P（2，1）的直线为(a＞0,b＞0),则.由基本不等式得,即ab≥8,,当且仅当,即a=4,b=2时，等号成立.故直线方程为,即x+2y-4=0.1xyab211ab212121abab142OABSab2112ab142xy学后反思(1)对直线的大致位置分析，界定了斜率的存在性及其范围，指明了解题方向，这种分析是避免解题盲目性的重要技能.（2）本题将面积表示为k的函数，再用基本不等式求最小值，方程选择不同，自然参数不同，但是...