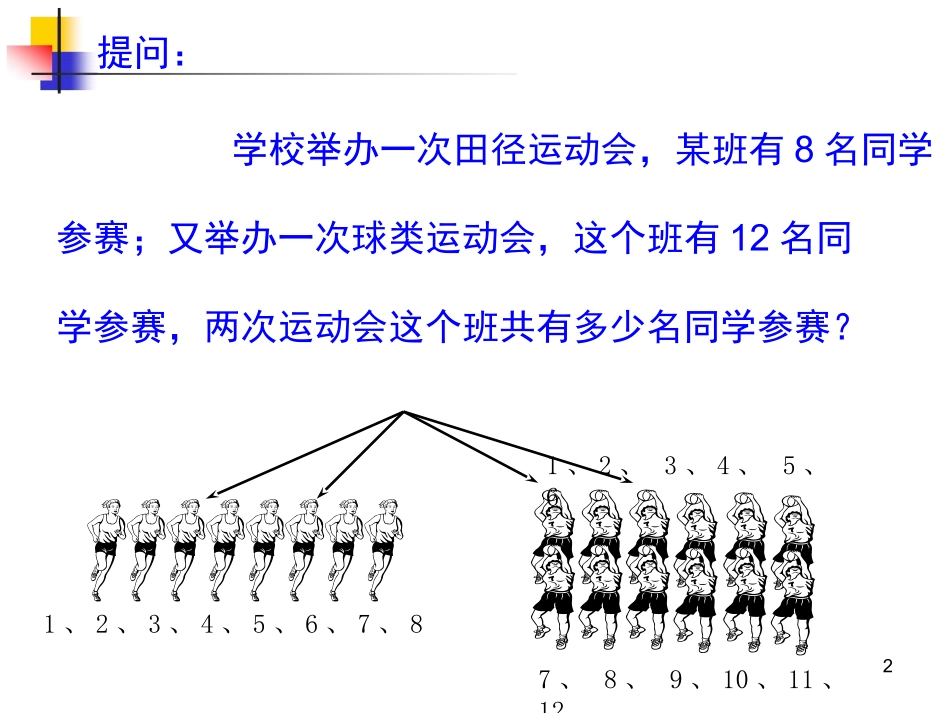
12学校举办一次田径运动会,某班有8名同学参赛;又举办一次球类运动会,这个班有12名同学参赛,两次运动会这个班共有多少名同学参赛?1、2、3、4、5、6、7、81、2、3、4、5、67、8、9、10、11、12提问:答:只有在所有参赛同学都只参加了一次运动会的情况下,回答有20名同学参赛。这就需要学习本章的集合与简易逻辑的知识,就可以描述和解决上述问题。集合与简易逻辑的初步知识是高中数学学习的重要基础。集合正数的集合负数的集合2X-1>3X>2所有x>2的实数组成这个不等式的解的集合。简称为这个不等式的解集初中我们把圆定义为到定点的距离等于定长的点的集合。几何图形都可以看作是点的集合。某些指定的对象集在一起就成为一个集合,简称集。例如:我校篮球队的队员北冰洋印度洋大西洋太平洋,,,我们经常用大写的字母来表示集合例如:北冰洋印度洋大西洋太平洋,,,A6,5,4,3,2,1B一、集合的概念6某些指定的对象集在一起就成为一个集合.集合的元素①确定性(是就是,不是就不是)②无序性(不用考虑次序)③互异性(元素不能重复)判别下列是否集合,说明理由:(1)班上的高个子同学;(2)数轴上非常靠近原点的点;(3)所有无限不循环小数;(4)方程x2-1<0的实数解.(5){1,2,3,4,5,1}(6){4,2,5,3,1,2}集合按元素数目分类:有限集,无限集,空集Φ.下面是一些常用的数集及其记法1)全体非负整数的集合通常简称非负整数集(自然数集)记作N非负整数集内排除0的集,称正整数集,记作N*或N+2)全体整数的集合通常简称整数集,记作Z3)全体有理数的集合通常简称有理数集,记作Q4)全体实数的集合通常简称实数集,记作R二、集合与元素的符号某些指定的对象集在一起就成为一个集合.集合的元素①确定性(是就是,不是就不是)②无序性(不用考虑次序)③互异性(元素不能重复)元素与集合的关系:从属(个体与整体)符号表示:a∈A(a属于集合A)集合的符号:集合A,B,C,……元素的符号:a,b,c,……aA或aA(a不属于集合A)集合中的每个对象叫做这个集合的元素fedcbaA,,,,,aA,AamA,Am例如:设B={1,2,3,4,5},那么B5B23又如:ZQN23,23,6练习:优化设计P2,随堂训练1、2、3、4、5、6属于记作不属于记作四、集合的表示方法(1)1,2,3,4,5(2)单位圆上所有的点(3)所有直角三角形(4)高一(15)班全体学生(5)方程x2-1=0的解(6)不等式x2-x-2>0的解——{1,2,3,4,5}——{单位圆上的点}——{直角三角形}——{高一(15)班学生}——{x|x2-1=0}或{±1}——{x|x2-x-2>0}1)列举法——把集合中的元素一一列举出来2)描述法——通过描述集合中所有元素的共同属性来表示集合(可以是文字,也可以是数学式){x|x所满足的性质}代表元素四、集合的表示方法3)图象法——韦恩图(或称文氏图)A14532特别注意!元素的无序性体现:{1,2,3,4,5}与{2,5,4,3,1}是同一个集合.元素的互异性体现:①{1,2,3,4,5,1}是错误的;②集合{a,b}中必须满足a≠b.用一条封闭曲线围成的区域表示一个集合四、集合的表示方法举例例用适当的方法表示下列集合(1)大于1小于10的偶数与质数所成的集合(2)正有理数集(3)偶数集奇数集正奇数集{x∈Q|x>0}{x|x=2n,n∈Z}{x|x=2n+1,n∈Z}{x|x=2n+1,n∈N*}作业:书本第6页:练习1、2优化设计第2页:7、8、9、10