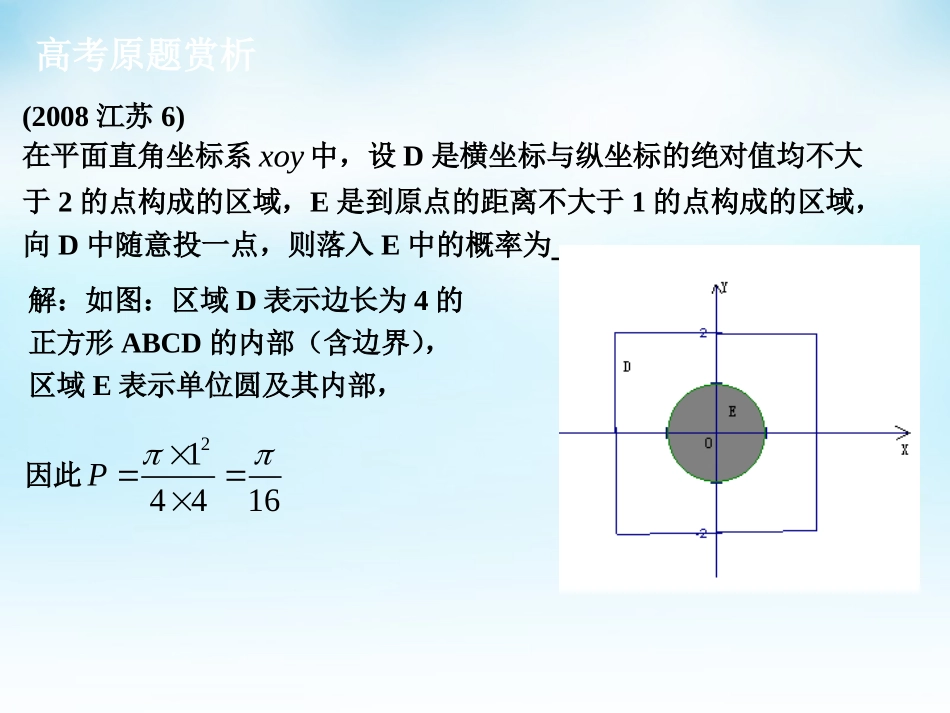
古典概型与几何概型高考原题赏析(2014江苏4)从1,2,3,6这4个数中一次随机地取2个数,则所取2个数的乘积为6的概率是.解:从1,2,3,6这4个数中任取2个数共有6种取法,其中乘积为6的有1,6和2,3两种取法,因此所求概率为2163P.高考原题赏析(2008江苏6)在平面直角坐标系xoy中,设D是横坐标与纵坐标的绝对值均不大于2的点构成的区域,E是到原点的距离不大于1的点构成的区域,向D中随意投一点,则落入E中的概率为。解:如图:区域D表示边长为4的正方形ABCD的内部(含边界),区域E表示单位圆及其内部,因此214416P一,学习目标:1.理解古典概型及其概率计算公式.会计算一些随机事件所含的基本事件数及事件发生的概率.2.理解几何概型的意义并会计算相应几何概型的问题的概率.要点梳理1.古典概型(1)概念:一般地,一次试验有下面两个特征①有限性.试验中所有可能出现的基本事件只有有限个;②等可能性.每个基本事件的发生都是等可能的,称这样的概率模型为古典概型.(2)公式:如果一次试验的等可能基本事件共有n个,那么每一个等可能基本事件发生的概率都是1n;如果某个事件A包含了其中m个等可能基本事件,那么事件A发生的概率为P(A)=mn.2.几何概型(1)概念:设D是一个可度量的区域,每个基本事件可以视为从区域D内随机地取一点,区域D内的每一点被取到的机会都一样;随机事件A的发生可以视为恰好取到区域D内的某个指定区域d中的点.这时,事件A发生的概率与d的测度(长度、面积、体积等)成正比,与d的形状和位置无关,则称这样的概率模型为几何概型.(2)公式:P(A)=d的测度D的测度.要点梳理3.古典概型与几何概型的区别(1)相同点:基本事件发生的可能性都是相等的;(2)不同点:古典概型的基本事件是有限个,是可数的;几何概型的基本事件是无限个,是不可数的.基础回顾1.若以连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标,则点P在直线x+y=5下方的概率为________.162.三张卡片上分别写上字母E,E,B,将三张卡片随机地排成一行,恰好排成英文单词BEE的概率为________.133.在长为12cm的线段AB上任取一点M,并且以线段AM为边作正方形,则这个正方形的面积介于36cm2与81cm2之间的概率为______.解: AM2∈[36,81],∴AM∈[6,9],∴P=9-612=312=14.4.在区间-π2,π2上随机取一个数x,cosx的值介于0到12之间的概率________.解:在区间[-π2,π2]内,0