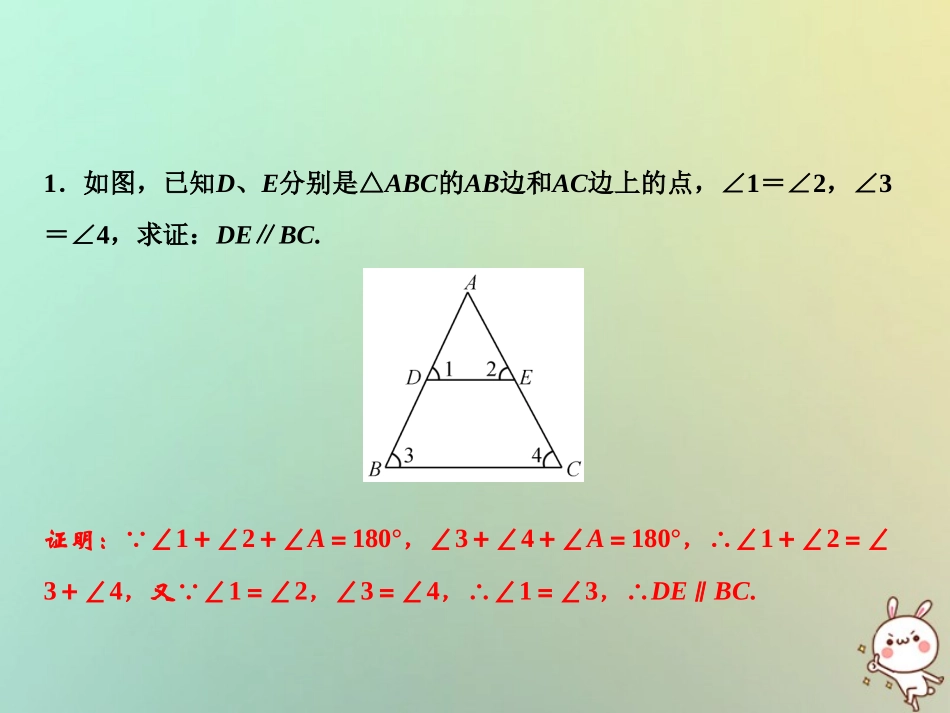
第13章三角形中的边角关系、命题与证明专题强化五三角形中求角度的两类图形2018秋季数学八年级上册•HK强化角度1“塔形”型如图是“塔形”模型的示意图,可利用结论:∠1+∠2=∠3+∠4求解相关问题.1.如图,已知D、E分别是△ABC的AB边和AC边上的点,∠1=∠2,∠3=∠4,求证:DE∥BC.证明:∵∠1+∠2+∠A=180°,∠3+∠4+∠A=180°,∴∠1+∠2=∠3+∠4,又∵∠1=∠2,∠3=∠4,∴∠1=∠3,∴DE∥BC.2.如图,已知D、E分别是△ABC的AB边和AC边上的点,∠B=50°,∠C=60°,求∠BDE+∠CED的度数.解:∵∠BDE与∠ADE互补,∠CED与∠AED互补,∴∠BDE+∠CED=(180°-∠ADE)+(180°-∠AED)=360°-(∠ADE+∠AED).∵∠ADE+∠AED=∠B+∠C=110°,∴∠BDE+∠CED=360°-110°=250°.强化角度2“对顶三角形”型如图是“对顶三角形”模型的示意图,其存在结论:∠1+∠2=∠3+∠4.3.如图所示,AC与BD交于点E,已知∠A=40°,∠B=45°,∠C=47°,则∠D等于()A.42°B.40°C.38°D.35°4.如图,在△ABC中,∠C=90°,AE平分∠BAC,BD⊥AE交其延长线于点D.若∠1=24°,则∠EAB的度数为()A.66°B.33°C.24°D.12°CC5.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.解:∵∠A+∠B+∠AIB=180°,∠C+∠D+∠CPD=180°,∠E+∠F+∠EOF=180°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠AIB+∠CPD+∠EOF=540°,又∵∠AIB+∠CPD+∠EOF=180°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.