高二数学下册 11.4(点到直线的距离)课件 沪教版 课件VIP免费

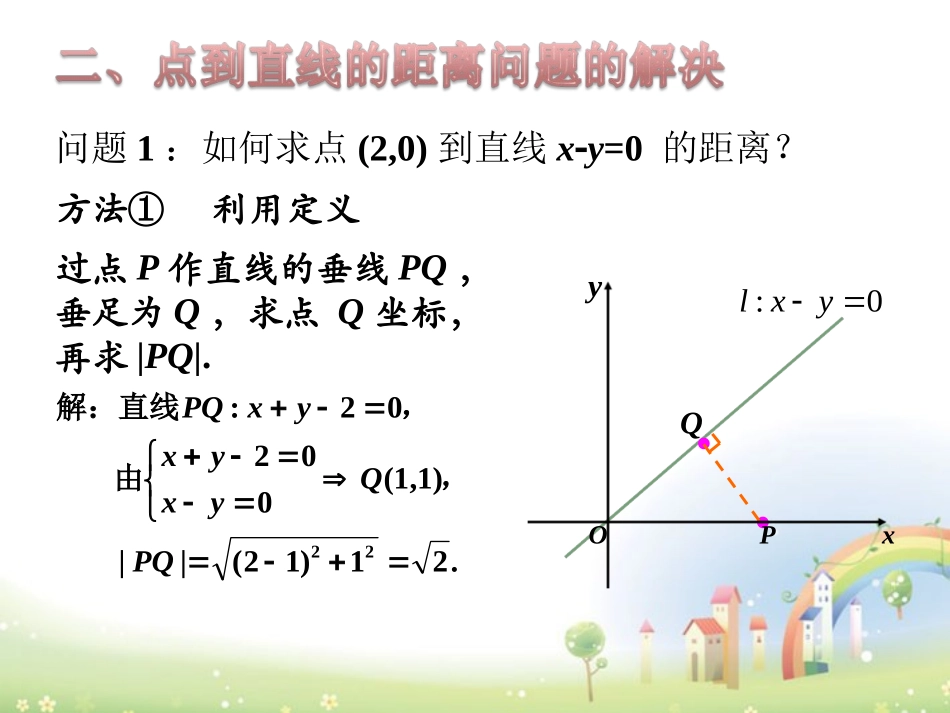
平面几何中点到直线的距离是怎样定义的？（1）点与直线的位置关系点在直线上和点在直线外两种位置关系。用点的坐标是否满足直线方程来判断点与直线的位置关系。（2）两点A(a1,b1)、B(a2,b2)之间的距离公式221221)()(||bbaaAB（3）点P到直线l的距离过点P作l的垂线，P与垂足P0之间的距离。问题1：如何求点(2,0)到直线xy=0的距离？:0lxy·方法①利用定义过点P作直线的垂线PQ，垂足为Q，求点Q坐标，再求|PQ|.·yOPxQ.21)12(||(1,1)00202:22PQQyxyxyxPQ，由，解：直线方法③利用直角三角形的面积公式方法②利用三角函数:0lxy··yOPxQ|PQ|=|OP|sin450=2sin450=2.2||,2||,22||),2,2(|,|||||||RtPQPRORRPROPPQOROPR中，R2,0PxyO:0lxy··00,Qxy·方法④利用函数的思想220022000200(2)442(1)2212.PQxyxxxxxQP.当时，设直线上的点Q(x0,y0)，Q方法①直接法xyOQ·问题2求点P0(x0,y0)到直线l:ax+by+c=0(a2+b20)的距离。直线l的方程直线l的方向QPl0直线l的方程直线P0Q的方程交点点P0、Q之间的距离|P0Q|（P0到l的距离）点P0的坐标直线P0Q的方向点P0的坐标点Q的坐标两点间距离公式思路简单运算繁琐P0l:ax+by+c=0xO方法②面积法·Q·RS··dy求出点R的坐标面积法求出|PQ|利用勾股定理求出|SR|求出|PR|求出PS求出点S的坐标P(x0,y0)l:ax+by+c=0过程设计Oxyl:ax+by+c=0P(x0,y0)Q方法③向量法设点P在直线l上的射影为Q(xQ,yQ)，||||||nnQPPQ),,(banl的法向量为直线,0夹角为与指向的同一侧，则的法向量在若点nQPnlP||||0cos||||nQPnQPnQP,夹角为与则指向的另一侧，的法向量在若点nQPnlP||||cos||||nQPnQPnQP2200|),(),(|babayyxxQQ2200|)()(|bayybxxaQQ2200|)()(|babyaxbyaxQQ2200||bacbyax点Q的坐标满足直线l的方程。例.求点P(1,2)到下列直线的距离：（1）y=2x+10；（2）3x=2；（3）2y+1=0,0102)1(yx化为直线的一般式：解：.5212|102)1(2|22d用点到直线的距离公式，先将直线方程化为一般式。OxyP32x35|)1(32|)2(d特殊状态的直线可数形结合解决。Oxy21yP25|)21(2|)3(d1.求点P(3,1)到下列直线的距离（1）3x+4y5=0；（2）5x+2=0；（3）3y1=0.5843|5433|(1)22d根据距离公式得解：517|)52(3|,52(2)dx32|311|,31(3)dy2.已知△ABC的三个顶点坐标分别为A(2,1)、B(5,3)、C(1,5)，求△ABC的BC边上的高。点A到BC所在直线的距离。解：直线BC的方程为x+3y14=0,.3131932|1432|22d根据距离公式得