高三数学署期补课件 第十五讲二次函数 新课标 人教版 课件VIP免费

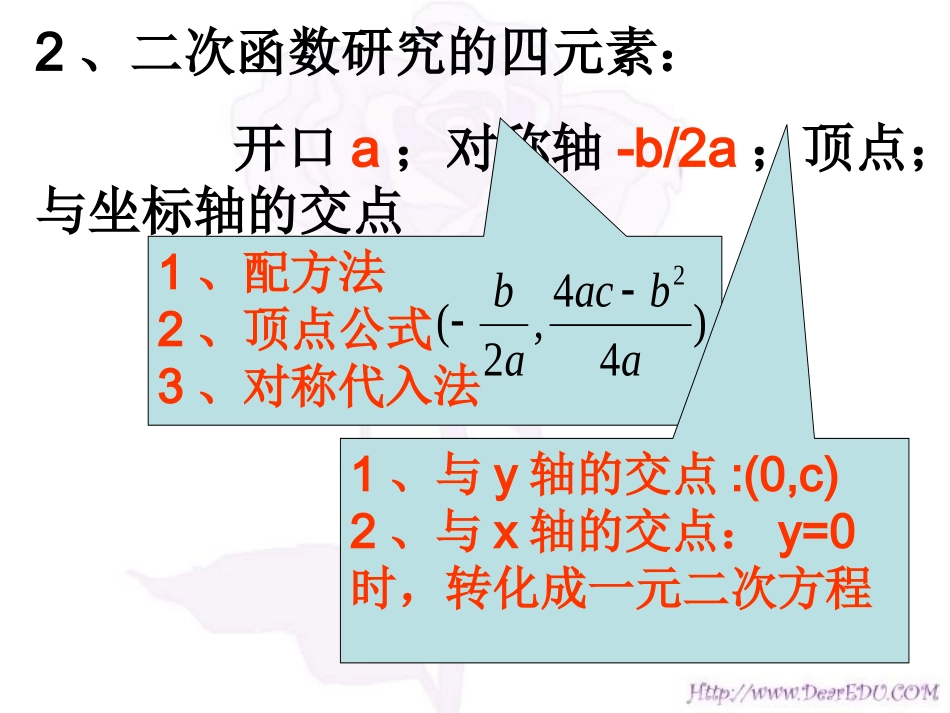
第十五讲二次函数基础知识•1、二次函数的解析式（待定系数法）•①一般式：y=ax2+bx+c(a≠0)•②顶点式：y=a(x－h)2+k,a≠0，其中(h,k)为抛物线的顶点坐标。•③零点式(两根式)：y=a(x－x1)(x－x2)，a≠0其中x1、x2是抛物线与x轴两交点的横坐标。2、二次函数研究的四元素：开口a；对称轴-b/2a；顶点；与坐标轴的交点1、配方法2、顶点公式3、对称代入法)44,2(2abacab1、与y轴的交点:(0,c)2、与x轴的交点：y=0时，转化成一元二次方程3、二次函数的相关量1）单调性的相关量：开口；对称轴2）最值相关量：10定义域R：20定义域[m,n]：3）对称轴相关量：10:对称轴x=-b/2a20:f(a)=f(b)(a≠b)对称轴x=(a+b)/2注：以静制动4）二次方程、二次不等式10与x轴的交点坐标是方程f(x)=0的实根，它在x轴上的线段长为||4)(||2122121axxxxxx20突现函数图象，研究二次方程ax2+bx+c=0的根的分布问题：①二次项系数a的符号；②判别式的符号；③区间端点函数值的正负；④对称轴x=－b/2a与区间端点的关系注：方程、不等式问题等价转化图形问题等价转化简单不等式组Δ=b2－4acΔ>0Δ=0Δ<0二次函数f(x)=ax2+bx+c(a>0)的图象一元二次方程ax2+bx+c=0(a≠0)的根一元二次不等式ax2+bx+c>0(a>0)的解集一元二次不等式ax2+bx+c<0(a>0)的解集有相异两实根x1,x2(x1x2x≠－b/2aRx125A变1：函数f(x)=-x2+ax+b2-b+1对任意实数x都有f(1-x)=f(1+x)成立，若当x[-1∈，1]时，f(x)>0,则b的范围？变2：函数f(x)=|x2-2ax+b|(xR).∈给出下列命题：①f(x)必是偶函数②当f(0)=f(2)时，f(x)的图象必关于x=1对称③若a2-b≤0则f(x)在区间[a,+∞)上是增函数④f(x)的最大值|a2-b|其中正确的序号是_____4.已知二次函数f(x)同时满足条件：•⑴f(1+x)=f(1－x)；•⑵f(x)的最大值为15；•⑶f(x)=0的两根立方和等于17，•求f(x)的解析式。待定系数法5.已知二次函数f(x)的定义域为R，f(1)=2，在x=t处取得最值，若y=g(x)为一次函数，且f(x)+g(x)=x2+2x－3。•⑴求f(x)的解析式；•⑵若x∈［－1,2］时f(x)≥－1恒成立，求t的取值范围。6、老师给出一个函数f(x)，四个学生甲、乙、丙、丁各指出这个函数的一个性质：甲：对于xR∈，都有f(1+x)=f(1－x)；乙：在（－∞，1］上函数递减；丙：在（－∞，1）上函数递增；丁：f(0)不是函数的最小值。如果其中恰有三个说的正确，请写出一个这样的函数_______________。变：若二次函数f1(x)=a1x2+b1x+c1和f2(x)=a2x2+b2x+c2，使得f1(x)－f2(x)在［1,2］上是单调减函数，且在［1,2］上有最大值5和最小值3。请写出一组满足上述要求的二次函数：f1(x)=_________,f2(x)=_______•7.已知实数a、b、c，函数f(x)=ax2+bx+c,g(x)=ax+b，当•－1≤x≤1时|f(x)|≤1.•⑴证明：|c|≤1；•⑵证明：当－1≤x≤1时|g(x)|≤2；•⑶设a＞0，当－1≤x≤1时g(x)的最大值为2，求f(x)。•例1求函数y＝x2―2ax―1在［0,2］上的值域。•变：已知函数f(x)=x2+ax+3－a，若x∈[－2,2]时，f(x)≥0恒成立，求实数a的取值范围。分类讨论等价于f(x)在[-2,2]的最值大于等于0二次函数在区间上的最值•若x≥0,y≥0,且x+2y＝1，则2x+3y2的最小值为（）•A.2B.3/4•C.2/3D.0B•例2、已知二次函数f(x)=ax2+bx+c和一次函数g(x)=－bx,其中a、b、c满足a>b>c，a+b+c=0(a、b、c∈R).•⑴求证：两个函数的图象交于不同的两点A、B；•⑵求线段AB在x轴上的射影A1B1之长的取值范围。2120accbacba解：(1)y=ax2+bx+c∴ax2+bx+c=-3xy=-bxax2+2bx+c=0①△=4b2-4ac=4(-a-c)2-4ac=4[(a+)2+c2] a>b>ca+b+c=0∴a>0c<0∴△>0∴两函数图象交于两个不同点。2c43（2）设方程两个根...