高二数学定积分应用课件 新课标 课件VIP免费

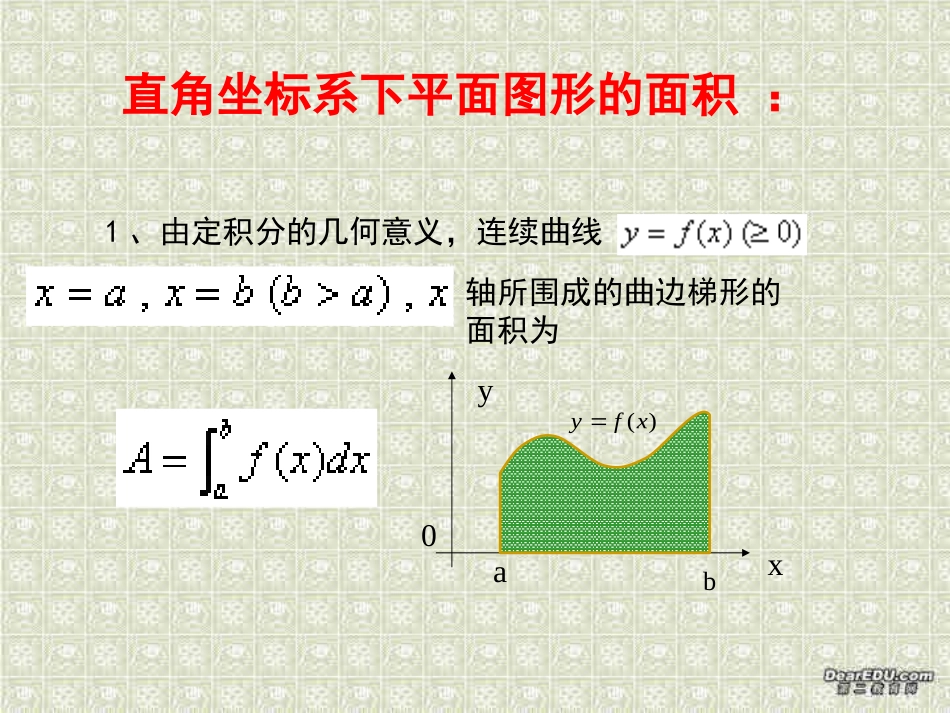
定积分的应用一.定积分的几何应用直角坐标系下平面图形的面积：1、由定积分的几何意义，连续曲线轴所围成的曲边梯形的面积为)(xfya0xyb负则围图图积为bacdacebde2f(x)[a,b],A=f(x)dx.=f(x)dx-f(x)dx+f(x)dx-f(x)dx.、若在上不都是非的所成形（如右）的面bo)(xfycdexyoayxo)(11xfy)(22xfyab、若平面区域是型区域：由上曲线、下曲线左直线、右直线所围成，则其面积公式为：1122b12a3xy=f(x)y=f(x)x=ax=bA=f(x)-f(x)dx.、若平面区域是型区域：由左曲线、右曲线、下直线、上直线11224yx=g(y)x=g(y)y=ay=b21,()().baAgygydy所围成则其面积公式为：如图所示。xyoab)(1ygx)(2ygx5、如果平面区域既不是x—型区域，也不是y—型区域，则用一组平行于坐标轴的直线，把平面区域分成尽可能少的若干个x—型区域与y—型区域，然后计算每一区域的面积，则平面区域总的面积等于各区域面积之和。如右下图：xEabABCDFGo显然：由图可以知道上部分曲线由三条不同的曲线：AB、BC与CD构成；下部分曲线由两条不同曲线：EF与FG所构成。为计算其面积，可分别过点B、C与F作平行于y轴的直线，这样则把平面区域分成4个x—型区域，然后利用前面的X——型区域的公式就可以计算了。下面看几个计算的例子我们就清楚利用定积分如何计算不规则图形的面积了。抛线线围区积们图2例求物y=x与直：x-2y-3=0所成的平面域的面.我可以先做出其形如下：AB1A2A分析1：所给的区域不是一个规范的x-域,如图为了便于计算需将其图形进行分割,即可化成两个x-形区域的面积问题。第一块的面积：1104[()]3Axxdx92112328[()]23323xAxdxAAA第二块的面积：则总面积：分析：若把围成的平面区域看成型区域：则左曲线为：右曲线为：下直线上直线为：直接由型区域面积的计算公式得面积232-12y-x=y,x=2y+3,y=-1,y=3y—2A=2y+3-ydy=10.31sincosyxyx练习：、，在[0，2]上所围成的面积。二.定积分在物理中的应用(1).变速直线运动的路程作变速直线运动的物体所经过的路程s,等于其速度函数v=v(t)(v(t)≥0)在时间区间[a,b]上的定积分,即()basvtdt例1一辆汽车的速度-时间曲线如图所示,求汽车在这1min内行驶的路程10102030203040506010ABCOv/m/st/s问题：物体在变力F(x)的作用下做直线运动，并且物体沿着与F(x)相同的方向从x=a点移动到x=b点，则变力F(x)所做的功为:()baWFxdx(2)、变力沿直线所作的功例2把一个带q电量的点电荷放在r轴上坐标原点处，它产生一个电场．这个电场对周围的电荷有作用力．由物理学知道，如果一个单位正电荷放在这个电场中距离原点为r的地方，那么电场对它的作用力的大小为2()qFxkr（k是常数），当这个单位正电荷在电场中从ar处沿r轴移动到br处时，计算电场力F对它所作的功．or解:roqab1r由题意,所求功为drrkqwba2barkq1.11bakq由物理学知道，质量分别为21,mm相距为r的两个质点间的引力的大小为221rmmkF，其中k为引力系数，引力的方向沿着两质点的连线方向．(3)、引力练习：P68A3，A5，B4作业题：P68A4，A6，B3