高一数学下册 61(正弦函数和余弦函数的图像与性质)课件 沪教版 课件VIP免费

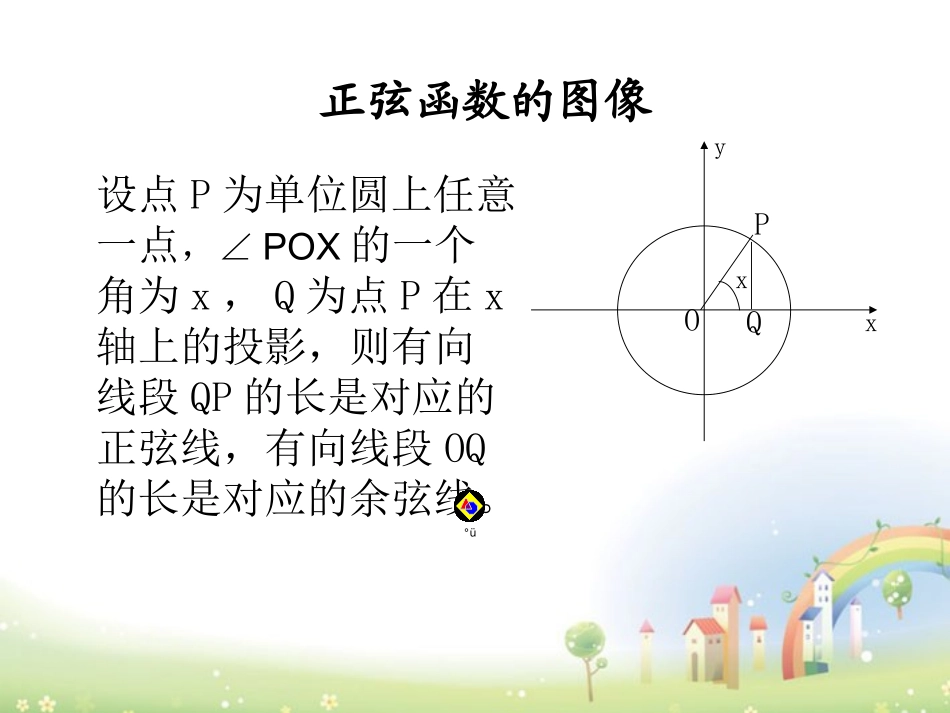
正弦函数和余弦函数的图像与性质1．复习：让学生口述函数的定义。2．引入：结合我们刚学过的三角比，就以正弦（或余弦）为例，对每一个给定的角和正弦值（或）之间是否也存在一种函数关系？若存在，请对这种函数关系下一个定义，若不存在请说明理由。3．讨论：对自变量的取值类型和范围进行讨论，并给出相应的正弦函数和余弦函数的记号。OxPyxQ正弦函数的图像设点P为单位圆上任意一点，∠POX的一个角为x，Q为点P在x轴上的投影，则有向线段QP的长是对应的正弦线，有向线段OQ的长是对应的余弦线。°ü讨论:在单位圆中正弦线和余弦线随角变化的变化有什么规律?请你设计如何来画正弦函数)2x0(xsiny的图像。同学作品演示unitµÄ¸±±¾.gsp（一）列表描点法画正弦函数图像：(1).列表2,0,sinxxyxy63232656734233561120212301212321230021231(2).描点(3).连线---223xy0211---一个周期内的正弦函数图像：归纳作正弦函数图象时的心得：先确定五点(0,0)，(2)，，，；再用光滑曲线连接，注意曲线弯曲特征；通过图像平移得到其他范围上的图像。)0,()1,2()1,23(---223xy0211---探究：我们已经有了正弦函数的图像，那我们如何得到余弦函数的图像？根据诱导公式我们知道)2sin(cosxx因此，要得到余弦函数的图像，我们只需要将正弦函数的图像向左平移个单位。xycos2y22xy22余弦函数图像：小结：比较这两种方法，第二种方法不仅简单，而且在此方法上我们可以得到许多与正弦函数有关的函数的图像。例1：用五点法作出下列函数图像|xsin|y)4例2：画出下列函数图像：][0,2xsin1)1xy],20[xxsiny)2]49,4[x)4xsin(y)3小结：(1)函数图像变换的方式：平移、对称；(2)平移分左右、上下平移，要注意平移的方向和平移的量。课堂小结今天你学到了什么？（1）正弦函数和余弦函数的定义（2）单位圆中的正弦线和余弦线（3）正弦函数和余弦函数的图像及其作法，简单的图像特征（4）函数图像平移中的方法及注意点1．书上练习1，2，32．书上习题6.1中的23．思考题：分别作出函数和的图像。作业布置xsin2yx2siny