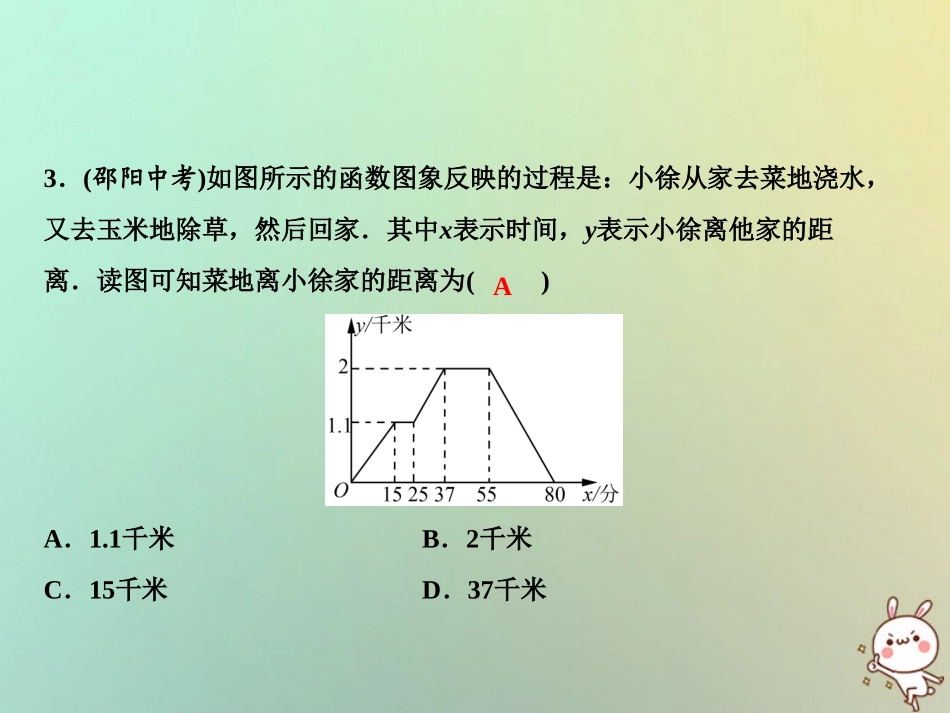
第四章综合检测题(时间:120分钟满分:120分)2018秋季数学八年级上册•B一、选择题(每小题3分,共30分)1.(六盘水中考)使函数y=3-x有意义的自变量x的取值范围是()A.x≥3B.x≥0C.x≤3D.x≤02.若正比例函数y=kx的图象经过点(1,2),则k的值为()A.-12B.-2C.12D.2CD3.(邵阳中考)如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为()A.1.1千米B.2千米C.15千米D.37千米A4.(大庆中考)对于函数y=2x-1,下列说法正确的是()A.它的图象过点(1,0)B.y值随着x值的增大而减小C.它的图象经过第二象限D.当x>1时,y>05.(上海中考)如果一次函数y=kx+b(k、b是常数,k≠0)的图象经过第一、二、四象限,那么k、b应满足的条件是()A.k>0且b>0B.k<0且b>0C.k>0且b<0D.k<0且b<0DB6.某油箱容量为60L的汽车,加满汽油后行驶了100km时,油箱中的汽油大约消耗了15,如果加满汽油后汽车行驶的路程为xkm,油箱中剩余油量为yL,则y与x之间的函数解析式和自变量取值范围分别为()A.y=0.12x,x>0B.y=60-0.12x,x>0C.y=0.12x,0≤x≤500D.y=60-0.12x,0≤x≤5007.(毕节中考)把直线y=2x-1向左平移1个单位,平移后直线的关系式为()A.y=2x-2B.y=2x+1C.y=2xD.y=2x+2DB8.(温州中考)已知点(-1,y1)、(4,y2)在一次函数y=3x-2的图象上,则y1、y2、0的大小关系是()A.0<y1<y2B.y1<0<y2C.y1<y2<0D.y2<0<y19.若函数y=2x+3与y=3x-2b的图象交x轴于同一点,则b的值为()A.-3B.-32C.9D.-94BD10.如图,在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,则R应运动到()A.M处B.N处C.P处D.Q处D二、填空题(每小题3分,共24分)11.若一次函数y=5x+m的图象过点(-1,0),则m=.12.已知直线l经过A(0,-1)、B(1,0)两点,则l的解析式为.13.(荆州中考)将直线y=x+b沿y轴向下平移3个单位长度,点A(-1,2)关于y轴的对称点落在平移后的直线上,则b的值为.14.已知一个函数,当x>0时,函数值y随着x的增大而减小,请写出这个函数关系式(写出一个即可).15.已知点P(a,b)在一次函数y=4x+3的图象上,则代数式4a-b-2的值等于.5y=x-14y=-x+2-516.已知一次函数y=-(k-1)x+5随着x的增大,y的值也随着增大,那么k的取值范围是.k<117.(锦州中考)已知A、B两地相距10千米,上午9∶00甲骑电动车从A地出发到B地,9∶10乙开车从B地出发到A地,甲、乙两人距离A地的距离y(千米)与甲所用的时间x(分)之间的关系如图所示,则乙到达A地的时间为.18.(雅安中考)定义:若两个函数的图象关于直线y=x对称,则称这两个函数互为反函数.请写出函数y=2x+1的反函数的解析式为.920∶y=12x-12三、解答题(共66分)19.(8分)已知y+2与x-1成正比例,且x=3时y=4.(1)求y与x之间的函数关系式;(2)当y=1时,求x的值.解:(1)设y+2=k(x-1),把x=3,y=4代入得4+2=k(3-1),解得k=3,则函数解析式是:y+2=3(x-1),即y=3x-5;(2)当y=1时,3x-5=1,解得x=2.20.(8分)根据如图图象回答问题.(1)写出A点坐标;(2)求出A、C两点的一次函数表达式;(3)直线AC与x轴交于点B,求S△BOC.(3,2)解:(2)y=43x-2;(3)当y=0时,x=32,∴OB=32,OC=2,∴S△OBC=12×32×2=32.21.(8分)甲、乙两地相距240千米,骑自行车以每小时20千米匀速从甲地出发,t小时后离乙地s千米.(1)写出s与t之间的函数关系式;(2)画出这个函数的图象;(3)回答:①8小时后距乙地多远?②出发后几小时,到两地距离相等?解:(1)s=240-20t(0≤t≤12);(2)画图象如右图;(3)①80千米,②6小时.22.(10分)已知,一次函数y=kx+3的图象经过点A(1,4).(1)求这个一次函数的解析式;(2)试判断点B(-1,5)、C(0,3)、D(2,1)是否在这个一次函数的图象上.解:(1) y=kx+3的图象经过A(1,4),∴k+3=4,∴k=1,∴一次函数的解析式为y=x+3;(2)B、D不在这个函数的图象上,...