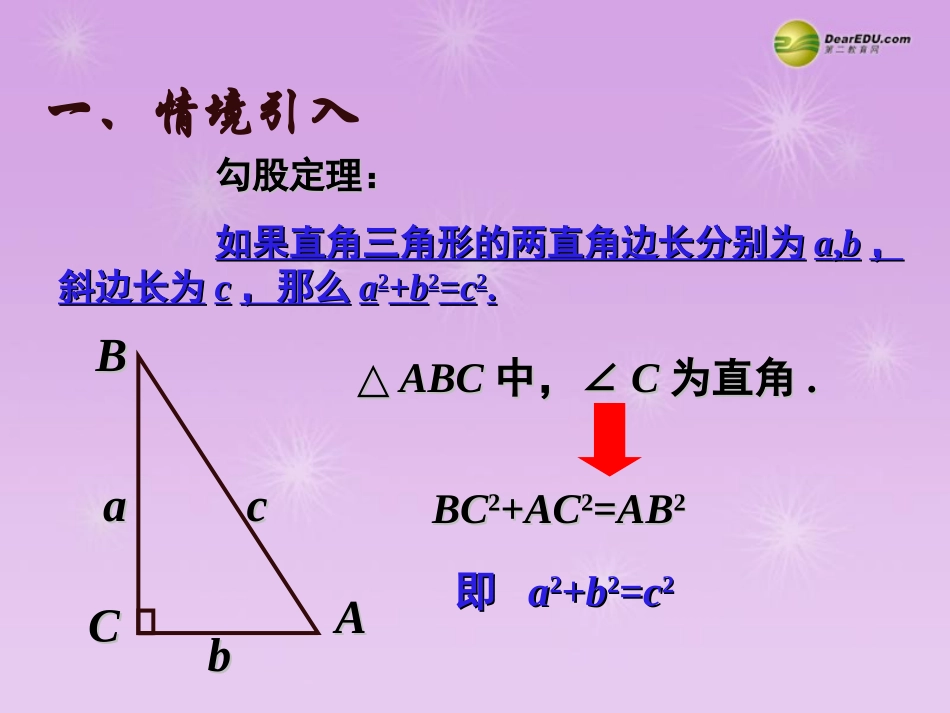
17.217.2勾股定理的逆定理勾股定理的逆定理第十七章勾股定理第第22课时课时一、情境引入勾股定理:勾股定理:如果直角三角形的两直角边长分别为如果直角三角形的两直角边长分别为aa,,bb,,斜边长为斜边长为cc,那么,那么aa22++bb22==cc22..aabbccCCAABB△△ABCABC中,∠中,∠CC为直角为直角..BCBC22++ACAC22==ABAB22即即aa22++bb22==cc22一、情境引入猜想:命题2如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.命题2正确吗?二、探究新知动手做一做!△ABC,其中a=3,b=4,c=5.△ABC是直角三角形吗?我们如何证明呢?方法一:剪一剪假如△ABC与画的直角三角形A′B′C′完全重合(全等)的话,能不能说明△ABC是直角三角形呢?AB45C334A′C′B′证明:画△△A′B′C′,使A′C′=4,B′C′=3,∠C′=90°,AB45C3∴A′B′=5,△△ABC,其中a=3,b=4,c=5.△△ABC是直角三角形吗?我们如何证明呢?34A′C′B′∴在△△ABC和△△A′B′C′中,AB=A′B′,AC=A′C′,BC=B′C′,∴△△ABC≌△△A′B′C′.∴∠C=∠C′=90°.即△△ABC是直角三角形.方法二:用推理证明的方法来论证两三角形是全等的.二、探索一般性的结论勾股定理的逆定理如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.古埃及人得到直角的方法通过证明,得到定理得到猜想画图(操作)验证问题:原命题成立,逆命题一定成立吗?你能举出一些相关的例子吗?一般地,如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理“互为逆定理”.原命题成立的,它的逆命题也可能不成立,如原命题成立的,它的逆命题也可能不成立,如命题命题““对顶角相等对顶角相等””成立,它的逆命题成立,它的逆命题““如果两个角如果两个角相等,那么这两个是对顶角相等,那么这两个是对顶角””不成立不成立..解:∵82+152=289,例判断由线段a,b,c组成的三角形是不是直角三角形.∴由线段a,b,c组成的三角形是直角三角形.应用新知a=15,b=8,c=17;a=13,b=14,c=15.172=289,∴a2+b2=c2,两条较短直角边的平方和较长直角边的平方能过成为直角三角形三条边长的三个正整数,称为勾股数.请举出两对互为逆定理的命题.三、巩固练习通过这节课的学习,你有什么收获?你还有什么困惑?四、小结1.必做题:教材习题17.2第3题.五、作业设计2.选做题:教材习题17.2第7题.(1)下列各组数中,不能组成直角三角形的是()3.备选题:A.4,40,41B.7,24,25C.13,84,85D.9,27,31(2)已知在△ABC中,AB=7,BC=24,AC=25,则=90°.(3)如右图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD,求证∠AEF=90°(提示:连接AF).