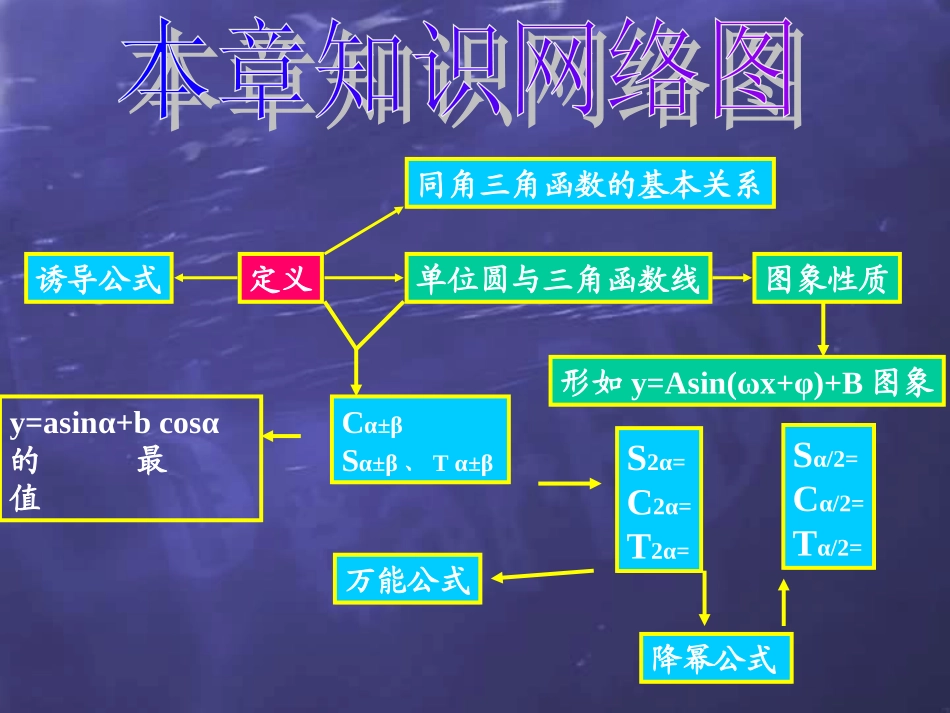
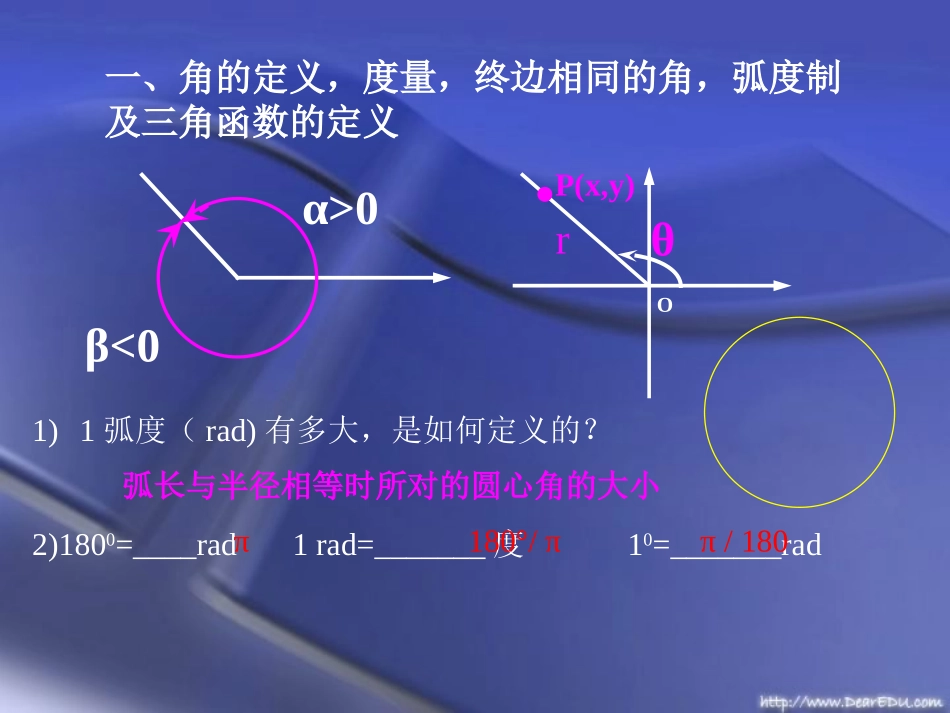
课题定义同角三角函数的基本关系图象性质单位圆与三角函数线诱导公式Cα±βSα±β、Tα±βy=asinα+bcosα的最值形如y=Asin(ωx+φ)+B图象万能公式Sα/2=Cα/2=Tα/2=S2α=C2α=T2α=降幂公式一、角的定义,度量,终边相同的角,弧度制及三角函数的定义α>0β<0O.θP(x,y)r1)1弧度(rad)有多大,是如何定义的?2)1800=____rad1rad=_______度10=_______rad弧长与半径相等时所对的圆心角的大小π180°/ππ/180111111222_____csc_____sec_____sin____sincostan____sincot________sec____cscαααααααααα二、同角三角函数的八大关系sinαcosαtanαcot2αtan2αcos2αcotαcosα二、两组诱导公式:①2kπ±α,π±α的三角函数值,等于α的同名三角函数值,前面加上把α看成锐角时原函数值的符号.②π/2±α,3π/2±α的三角函数值,等于α的余名三角函数值,前面加上把α看成锐角时原函数值的符号.三、一般函数图象变换基本变换位移变换伸缩变换上下平移左右平移上下伸缩左右伸缩y=f(x)图象y=f(x)+b图象y=f(x+φ)图象y=Af(x)图象y=f(ωx)图象向上(b>0)或向下(b<0)移︱b︱单位向左(φ>0)或向右(φ<0)移︱φ︱单位点的横坐标变为原来的1/ω倍纵坐标不变点的纵坐标变为原来的A倍横坐标不变四、记住下列三角公式::sin()sincoscossincos()coscossinsintantantan()1tantan①两角和与差的正弦、余弦、正切αβαβαβαβαβαβαβαβαβ22222:2tansin22sincos;tan21tancos2cossin12sin2cos1②二倍角公式ααααααααααα天哪!22cos1sin;22cos1cos:22αααα③降幂公式:1cos1coscos;sin22221cossin1costan21cos1cossin④半角公式ααααααααααα222:2tan1tan22sin;cos1tan1tan22⑤万能公式αααααα⑥和差化积与积化和差公式不需记但要会用.吔!三角解题常规宏观思路分析差异寻找联系促进转化指角的、函数的、运算的差异利用有关公式,建立差异间关系活用公式,差异转化,矛盾统一1、以变角为主线,注意配凑和转化;2、见切割,想化弦;个别情况弦化切;3、见分式,想通分,使分母最简;4、见平方想降幂,见“1±cosα”想升幂;5、见sin2α,想拆成2sinαcosα;6、见sinα±cosα或想平方再转化7、见asinα+bcosα,想化为形式φα)sin(ba22微观直觉sinα+sinβ=pcosα+cosβ=q..;.;.;.)(coscos第四象限第三象限第二象限第-象限角属于α则,α|α|α角是第二象限且满足设例DCBA2221C点评:本题先由α所在象限确定α/2所在象限,再α/2的余弦符号确定结论.11228222.;.;.;.)(cossinDCBAaxxaxy等于对称,那么π的图像关于直线如果函数例思路:函数y=sin2x+acos2x可化为)2sin(12φxay要使它的图象关于直线x=-π/8对称,则图象在该处必是处于波峰或波谷.即函数在x=-π/8时取得最大、小值.Daaa,应选解得|ππ由|解11)8(2cos)8(2sin:2到?的平移和伸缩变换而得的图象经过怎样,②该函数图象可由的集合大值时,求自变量取得最①当函数,已知函数例RxxyxyRxxxysin;cossin33解题步骤:分,π化函数为3Rx)6xsin(2y.1分ππ|的集合为取最大值时得6}Zk,3k2xx{xy.2分图象π,得到π图象向左平移①将9)6sin(6sinxyxy分的图象π得到倍伸长到原来的标的横坐标不变,把纵坐②将所得图象上所有点12.)6/xsin(2y,23.指出变换过程:431sin(,)tan(),522tan(2).例π已知α,απ,π-β求α-β值:sincostan;解题步骤①由α值求出α值,得出α值tan()tantan2;②由πβ值,求出β值,再求β值tan(2).③再利用差角公式求出αβ值答案:tan(α-2β)=7/24..cossincossin值求例5020502052222cos1cos22cos1sin22αα,αα①利用降幂公式基本思路:)]sin()[sin(21cossinβαβαβα②利用积化和差公式2sin2sin2coscosβαβαβα③利用和差化积公式最后结果:43原式.coscoscoscos,,的值,求,,满足中,三内角...