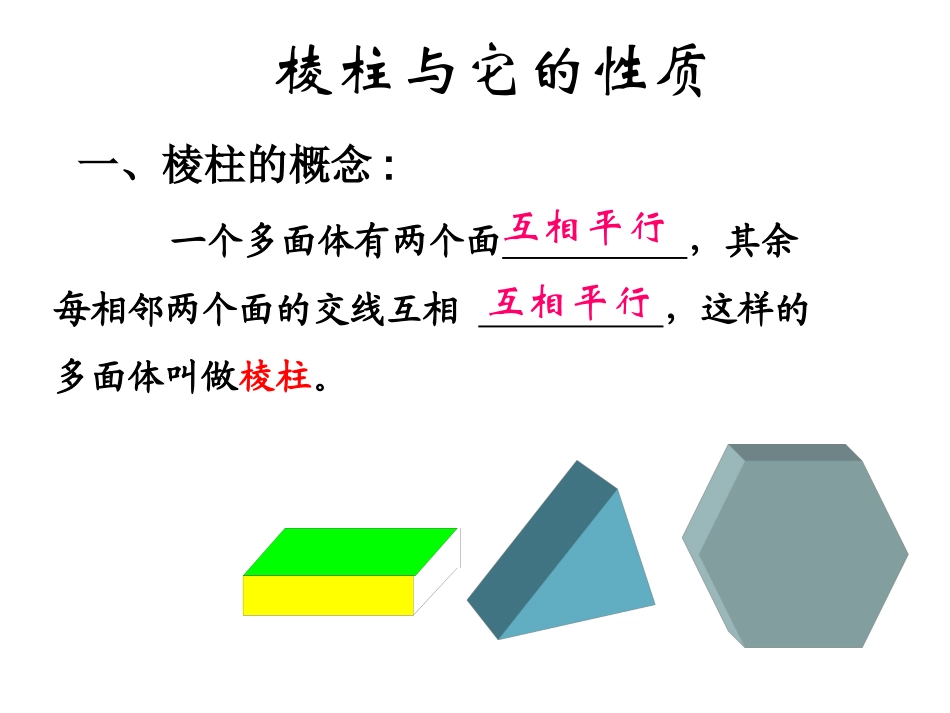
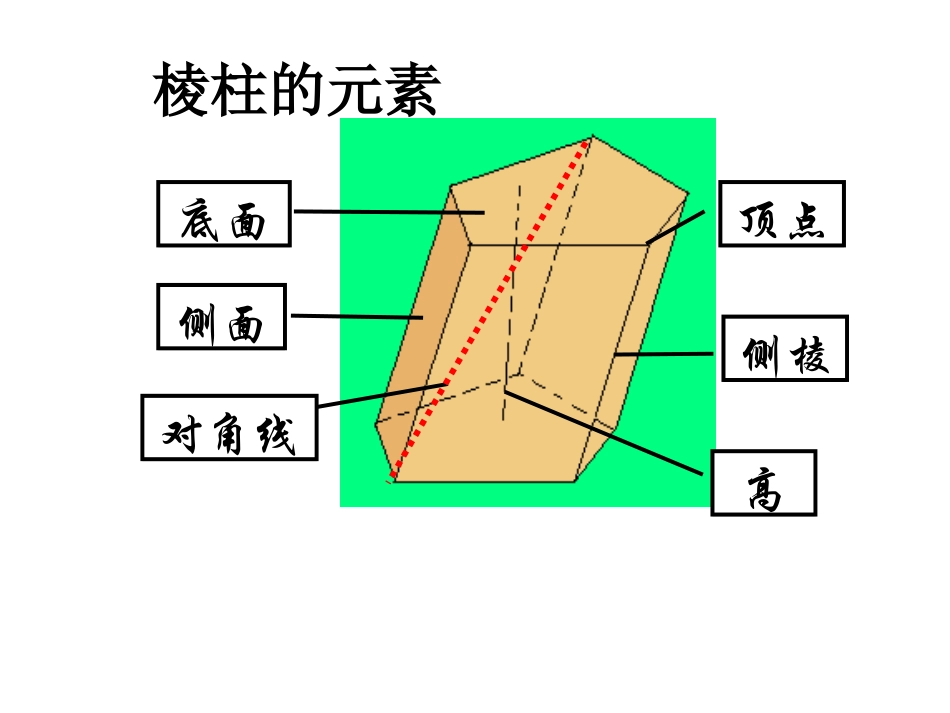
棱柱与它的性质一、棱柱的概念:一个多面体有两个面,其余每相邻两个面的交线互相,这样的多面体叫做棱柱。互相平行互相平行底面对角线高侧面侧棱顶点棱柱的元素练一练练一练练一练练一练面数最少的棱柱是棱柱。它有个面,其中个底面、个侧面,它有条棱,其中条侧棱,它有个顶点,条对角线三52393606-9+(3+2)=2N(N是正整数)棱柱有个面,其中个底面、个侧面,有条棱,其中条侧棱,有个顶点,条对角线N+2N23NN2NN(N-3)ABCC1A1B12N-3N+(N+2)=2欧拉定理:点-线+面=2二二..棱柱的分类棱柱的分类ABCDEA’B’C’D’E’(1)侧棱不垂直于底面的棱柱叫做斜棱柱按侧棱与底面的关系分(2)侧棱垂直于底面的棱柱叫做直棱柱(3)底面是正多边形的直棱柱叫做正棱柱棱柱的底面可以是三角形、四边形、五边形、……把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……三棱柱四棱柱五棱柱棱柱的分类棱柱的分类按底面的形状分:斜三棱柱直四棱柱正五棱柱1、侧棱不垂直于底面且底面为三角形的棱柱叫做___________;2、侧棱垂直于底面且底面为四边形的棱柱叫做____________;3、侧棱垂直于底面且底面为正五边形的棱柱叫做____________。练一练练一练练一练练一练B5、一个棱柱是正四棱柱的条件是:A底面是正方形有两个侧面是矩形B底面是正方形有两个侧面垂直于底面C底面是菱形且有一个顶点处的三条棱两两垂直D每个侧面都是全等矩形的棱柱(C)4、下列命题之中的假命题是()A、直棱柱的侧棱是直棱柱的高。B、有一个侧面是矩形的棱柱是直棱柱。C、直棱柱的侧面是矩形。D、有一条侧棱垂直与底面的棱柱是直棱柱。11、棱柱:、棱柱:①①侧棱都侧棱都,侧面和对角面都是,侧面和对角面都是;;②②两个底面与平行于底面的截面是两个底面与平行于底面的截面是。。22、直棱柱、直棱柱:①①各侧面和各对角面都是各侧面和各对角面都是;;②②侧棱长与高侧棱长与高。。三.棱柱、直棱柱、正棱柱的性质33、正棱柱、正棱柱:①①底面是底面是;;②②各侧面都是各侧面都是。。平行且相等平行四边形全等多边形矩形相等正多边形全等的矩形四棱柱平行六面体长方体直平行六面体正四棱柱正方体底面变为平行四边形侧棱与底面垂直底面是矩形底面为正方形侧棱与底面边长相等四四..几种常见六面体的关系:几种常见六面体的关系:6.设M=正四棱柱,N=长方体,P=直四棱柱,Q=正方体,则这些集合间的关系是()PMNQQMNPPNMQQNMPA.B.C.D.B练一练练一练练一练练一练7.四棱柱成为平行六面体的一个充分而不必要条件是()A.侧面是平行四边形;B.底面是平行四边形;C.两相邻侧面是矩形;D.各侧面都是菱形.D练一练练一练练一练练一练平行六面体的性质平行六面体的性质::1.1.平行六面体的对棱平行且相等.2.平行六面体的对角线交于一点,并且在交点处互相平分。ABCDA'B'C'D'O定理长方体的对角线都相等。一条对角线的平方等于一个顶点上三条棱长的平方和。已知:长方体AC’中,AC’是一条对角线(如图)求证:AC'2=AB2+AD2+AA'2BCDAB'C'D'A'即:l2=a2+b2+c2abcl例1练习:1、已知一个长为体共顶点的三个面的面积分别为、、,求长方体的对角线的长。2362、已知长方体的全面积为22,所有棱长之和为24,求长方体的对角线长。例2的长。和,求对角线,中,各棱长均为如图,直平行六面体11160ACBDDABaACODCAB1A1D1C1B例3.)2(,)1(,6,2:111111的距离到平面求点的大小求二面角侧棱长为边长为的底面正四棱柱已知CABBBACBDCBAABCDABCDA1B1C1D1oE例4已知:正三棱柱ABC-A‘B’C‘的各棱长都为1,M是底面BC边上的中点,N是侧棱CC’上的点且CN=1/4CC‘。求证:AB'MN⊥C'CA'B'ABA'B'ABMN证明:∴B'MMN⊥,∴AB'MN.⊥∵M是中点在直三棱柱ABC-ABC中,∴AMBC⊥.易证RtMBB△'RtNCM∽△∴AM⊥面BC'.已知直三棱柱ABC-A1B1C1中,90ACB11,3,6,CBCAAAM是CC1的中点求证:1.BAAMMA1C1BCAB1练习:补充练习1:有一矩形纸片ABCD,AB=5,BC=2,E,F分别是AB,CD上的点,且BE=CF=1,把纸片沿EF折成直二面角.(1)求BD的距离;(2)求证AC,BD交于一点且被这点平分.补充练习2:如图:将长AD=√2,宽AB=1的长方形ABCD沿折痕折成一个正三棱柱的侧面,对角线AC成了正三棱柱上的折线段。求此折线段相邻两段所成的角。AC2C1BB1B2EFAC1C2DBB1B2CEF练习(最短路径问题)