高考数学专题复习25三角公式课件VIP免费

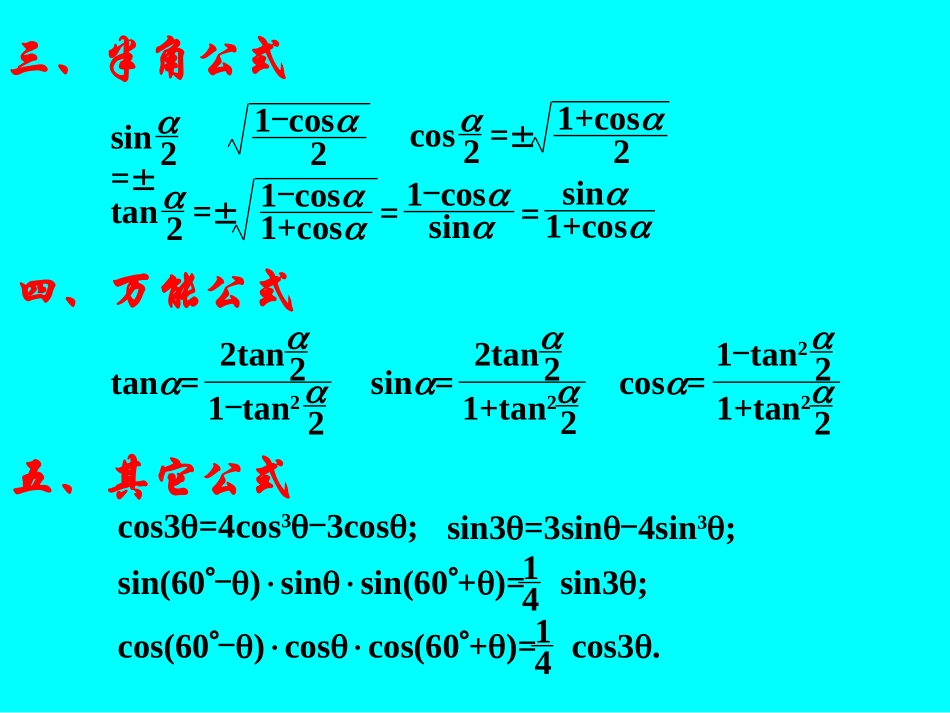
一、两角和与差的三角函数二、二倍角公式(升幂公式)(降次公式)sin()=sincoscossincos()=coscossinsin-+tan()=tantan1tantan-+asin+bcos=a2+b2sin(+)cos2=cos2-sin2=2cos2-1=1-2sin2sin2=2sincostan2=2tan1-tan2sin2=1-cos22cos2=1+cos22三、半角公式四、万能公式五、其它公式sin3=3sin-4sin3;cos3=4cos3-3cos;sin(60-)sinsin(60+)=sin3;14cos(60-)coscos(60+)=cos3.14sin=1-cos22cos=1+cos22tan=1-cos1+cos2=sin1+cos=1-cossinsin=2tan21+tan22tan=2tan21-tan22cos=1-tan221+tan22公式选择1.从函数的名称考虑切割化弦(有时也可考虑“弦化切”),异名化同名(使函数的名称尽量统一);2.从角的特点考虑异角化同角,抓住角之间的规律(如互余、互补、和倍关系等等);3.从变换的需要考虑达到分解、化简或将条件与结论挂钩等目的;4.尽量避开讨论常用技巧与方法1.变换常数项将常数变换成三角函数;2.变角对命题中的某些角进行分拆，从而使命题中的角尽量统一;3.升幂或降次运用倍、半角公式进行升幂或降次变换,从而改变三角函数式的结构;4.运用代数变换中的常用方法因式分解、配方、凑项、添项、换元等等.www.jkzyw.com三角函数式化简目标1.项数尽可能少;2.三角函数名称尽可能少;3.角尽可能小和少;4.次数尽可能低;5.分母尽可能不含三角式;6.尽可能不带根号;7.能求出值的求出值.典型例题1.求sin220º+cos250º+sin20ºcos50º的值.思维精析从幂入手,用降幂公式.解法1原式=++(sin70º-sin30º)1+cos100º21-cos40º212=-sin70ºsin30º+sin70º1234=.34思维精析从形入手,配成完全平方.=.3412解法2原式=(sin20º+cos50º)2+cos250º3412=[sin(50º-30º)+cos50º]2+cos250º34=(sin50ºcos30º)2+cos250º34思维精析从角入手,化异角为同角.=.34解法3原式=sin2(50º-30º)+cos250º+sin(50º-30º)cos50º=(sin50ºcos30º-cos50ºsin30º)2+cos250º+(sin50ºcos30º-cos50ºsin30º)cos50º=(sin250º+cos250º)34思维精析从式入手,构造对偶式.解法4设x=sin220º+cos250º+sin20ºcos50º,=.34思维精析从三角形入手,构造图形,利用正余弦定理.解法5设△ABC外接圆半径为1,A=20º,B=40º,y=cos220º+sin250º+cos20ºsin50º.则x+y=2+sin70º,①x-y=-cos40º+cos100º-sin30º.②x=(2+sin70º-cos40º+cos100º-sin30º)12=(+sin70º-2sin70ºsin30º)1232则C=120º.由正余弦定理知:原式=sin220º+sin240º+sin20ºsin40º=sin220º+sin240º-2sin20ºsin40ºcos120º=sin2120º=.34得:2①+②∴sin220º+cos250º+sin20ºcos50º的值为.341.求sin220º+cos250º+sin20ºcos50º的值.2.已知<<<,cos(-)=,sin(+)=-,求sin2的值.243131235解: <<<,243∴0<-<,<+<.423∴sin(-)=,cos(+)=-,45135∴sin2=sin[(+)+(-)]=sin(+)cos(-)+cos(+)sin(-)=-+(-)351312451356556=-.∴sin(-)>0,cos(+)<0,3.已知sin+cos=2sin,sincos=sin2,求证:2cos2=cos2.4.已知sin=msin(2+),其中m0,2+k(kZ),求证:tan(+)=tan.1-m1+m证: sin+cos=2sin,∴(sin+cos)2=4sin2.∴1+2sincos=2(1-cos2). sincos=sin2,∴1+2sin2=2(1-cos2).∴1+1-cos2=2(1-cos2).∴2cos2=cos2.证: sin=msin(2+),∴m=.sinsin(2+)=tan(+).∴tan=tan1-m1+msin(2+)+sinsin(2+)-sin=tan2sin(+)cos2cos(+)sin∴tan(+)=tan.1-m1+m另证: sin=msin(2+),∴sin[(+)-]=msin[(+)+].∴sin(+)cos-cos(+)sin整理得(1-m)sin(+)cos=(1+m)cos(+)sin.=m[sin(+)cos+cos(+)sin].∴tan(+)=tan.1-m1+m4.已知sin=msin(2+),其中m0,2+k(kZ),求证:tan(+)=tan.1-m1+m5.已知tan,cot...