高二数学：(解斜三角形的应用与举例)(林庆荣)课件 旧人教版 课件VIP免费

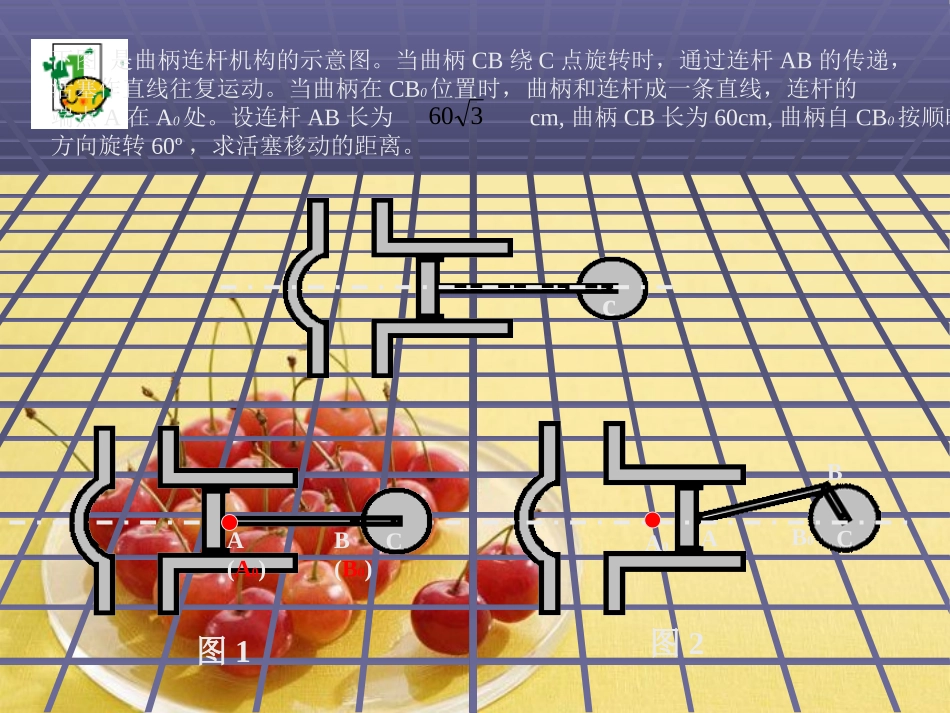
平南县大安高中林庆荣平南县大安高中林庆荣正弦定理余弦定理RCcBbAa2sinsinsin（R为三角形的外接圆半径）CabbacBcaacbAbccbacos2cos2cos2222222222abcbaCcabacBbcacbA2cos2cos2cos222222222ABCacb下图是曲柄连杆机构的示意图。当曲柄CB绕C点旋转时，通过连杆AB的传递，活塞作直线往复运动。当曲柄在CB0位置时，曲柄和连杆成一条直线，连杆的端点A在A0处。设连杆AB长为cm,曲柄CB长为60cm,曲柄自CB0按顺时针方向旋转60º，求活塞移动的距离。360B(B0)CA(A0)图1CBAB0A0图2c解：2136060sin60sinsin0ABCBCAABC中由正弦定理可得在009030BAAABBC为锐角cmBCAC12030sin0ACCAAA00。）（答：活塞移动的距离为cm60360A0AB0BC60º36060)(60360)(cmACBCAB某海轮以30海里/时的速度航行，在A点测得海面上油井P在南偏东，向北航行40分钟后到达B点测得油井P在南偏东，海轮改为北偏东的航向再行驶80分钟到达C点，求P、C两点的距离。060030060。CPBPBCPCPBCBCBPCBPBPABBAPAPBABABP海里两点的距离为、答：（海里））（由已知（海里）中，在（海里）由正弦定理可得（海里）中，在7207203204090603018040608030320120sin30sin120,30,20604030222200000000解：CABP北60º60º30º0300120我海军舰艇在A处获悉某渔船发出的求救信号后，立即测出该渔船在方位角（指由正北方向顺时针旋转到目标方向的水平角）为，距离A为10海里的C处，并测得渔船正沿方位角的方向以9海里/时速度向某岛P靠拢，我海军舰艇立即以21海里/时的速度前去营救，试问舰艇应按照怎样的航向前进？并求出靠近渔船所用时间。0450105北北BCA045010510X21X9解：。则小时，处靠近渔船所用的时间设舰艇从10,9,21ACxBCxABxA0000120)105180(45ACB010936120cos9102)9(1021120cos2202220222xxxxxBCACBCACAB即）则（由余弦定理可得)(125,3221舍去解得xx10142610142cos69,1421222222ACABBCACABBACxBCxAB再由余弦定理可得9286.0078.21BAC00078.6678.2145小时。近渔船需要的方位角方向航行，靠答：舰艇应以3278.660如下图，已知半圆的直径AB=2，点C在AB的延长线上，BC=1，点P为半圆上的动点。以PC为边作等边PCD，且点D与圆心O分别在PC的两侧，求四边形OPDC的面积的最大值。CPDOAB解：。，四边形的面积为设yPOBcos2222OCOPOCOPPCPOC中，由余弦定理得则在cos45PCDOPCSSy435cos3sin)cos45(3sin21sin2121435)3sin(2435)cos23sin21(243526523maxy时，即当BCDA03003006004523解：000000045sin30sin45456030180CDBCDBCBCD由正弦定理可得）（中，在kmBC46kmDCACACDADCADC23600中，在km。BAkmABBCACBCACABABC４６两点的距离为、答：中，由余弦定理可得在46832246232834345cos20222如何测量河对岸A、B两点的距离。(工具:皮尺,测角仪)思考总结：解应用题的基本模式：实际问题数学问题解答问题数学解