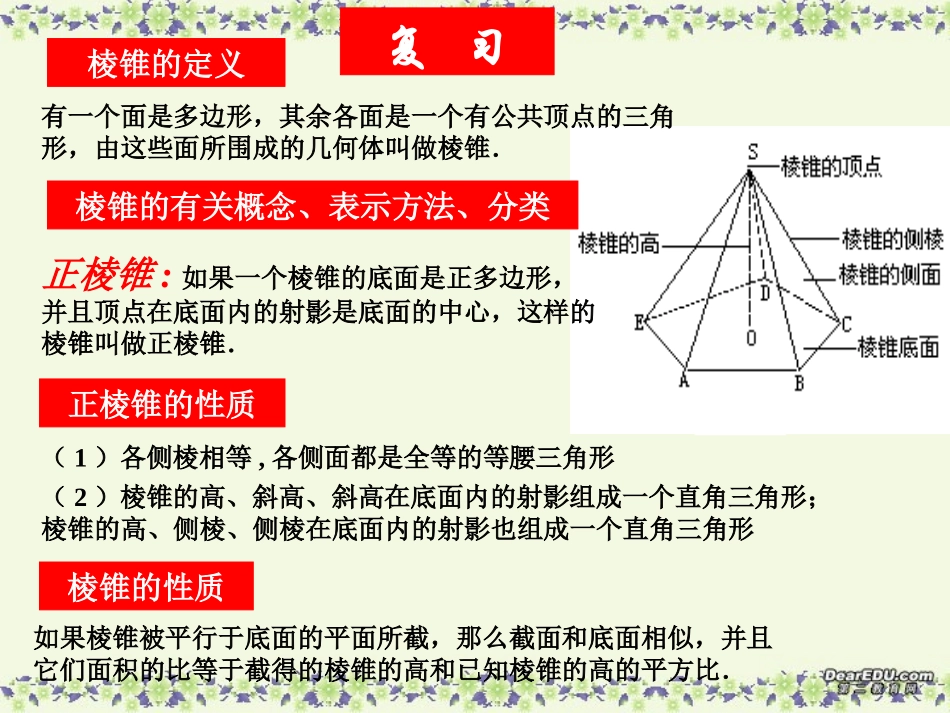
1、掌握棱锥定义及其有关概念、表示方法;2、熟练掌握棱锥性质;3、熟练掌握正棱锥定义及其性质;4、正确应用棱锥的概念及性质。复习棱锥的定义有一个面是多边形,其余各面是一个有公共顶点的三角形,由这些面所围成的几何体叫做棱锥.棱锥的有关概念、表示方法、分类正棱锥的性质(1)各侧棱相等,各侧面都是全等的等腰三角形(2)棱锥的高、斜高、斜高在底面内的射影组成一个直角三角形;棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形正棱锥:如果一个棱锥的底面是正多边形,并且顶点在底面内的射影是底面的中心,这样的棱锥叫做正棱锥.棱锥的性质如果棱锥被平行于底面的平面所截,那么截面和底面相似,并且它们面积的比等于截得的棱锥的高和已知棱锥的高的平方比.问题提出:如图是正方体的直观图如何把立体图形画在纸上?实质:把本来不完全在同一平面内的点的集合,用同一平面内的点来表示.复习回顾①斜二测画法规则②直棱柱直观图画法:先作水平放置的多边形直观图,再画一条与X轴垂直的Z轴,把平行于Z轴的线段保持长度与平行性不变.(以正六棱柱为例)斜二测画法规则:(1)在已知图形中取互相垂直的x轴和y轴,两轴交于点O.画直观图时,把它们画成对应的x1轴和y1轴,两轴交于点O1,使∠x1O1y1=450,它们确定的平面表示水平面。(2)1、在已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行x1轴或y1轴的线段。2、在已知图形中平行于x轴的线段,在直观图中保持原来长度不变;平行于y轴的线段,长度为原来的一半。(3)画一个与x轴、y轴都垂直的z轴,在直观图中平行于z轴的线段的平行性和长度都不变。步骤:1、画轴;2、画底面;3、画侧棱;4、成图。例1:正六棱柱的直观图的画法zノyノxノoノ步骤:1、画轴;2、画底面;3、画侧棱;4、成图。例1:正六棱柱的直观图的画法zノyノxノoノACDEFB步骤:1、画轴;2、画底面;3、画侧棱;4、成图。例1:正六棱柱的直观图的画法zノyノxノoノACDEFBFノEノAノDノBノCノ步骤:1、画轴;2、画底面;3、画侧棱;4、成图。例1:正六棱柱的直观图的画法zノyノxノoノACDEFBFノEノAノDノBノCノ步骤:1、画轴;2、画底面;3、画侧棱;4、成图。例1:正六棱柱的直观图的画法正棱锥的直观图与正棱柱的画法一样,由底面与高来决定,底面图形的画法即平面直观图的画法,高的画法是过底面中心作底面的垂线,其长度即为原棱锥的高,垂线段的另一端点即为正棱锥的顶点A1B1E1C1·D1o1S例2:作一个底面边长为5cm,高为11.5cm的正五棱锥直观图。(比例尺1:5)比例尺:图上和实际距离的比xyoMABCDENA1B1·M1·N1E1C1·D1y1x1o1y1x1A1B1E1C1·D1o1zSA1B1E1C1·D1o1S例2:作一个底面边长为5cm,高为11.5cm的正五棱锥直观图。(比例尺1:5)1.棱锥的一个平行于底面的截面把棱锥的高截成1:2,那么这个截面把棱锥的侧面分成两部分的面积比等于[]A.19∶B.18∶C.14∶D.13∶2.正三棱锥底面边长为a,侧棱与底面成45°角,求此棱锥的侧面积.练习:PDCBAB4152a1534162223.底面为矩形的四棱锥P-ABCD,PA⊥底面ABCD,PA=3cm,AB=4cm,BC=3cm,求棱锥P-BCD的侧面积.4.在正方体ABCD-A’B’C’D’中,已知棱长为a,求:(1)三棱锥B’-ABC的体积;(2)这个三棱锥的体积是正方形体积的几分之几;(3)B到平面AB’C的距离.361a61a33小结棱锥的定义有一个面是多边形,其余各面是一个有公共顶点的三角形,由这些面所围成的几何体叫做棱锥.棱锥的有关概念、表示方法、分类正棱锥的性质(1)各侧棱相等,各侧面都是全等的等腰三角形(2)棱锥的高、斜高、斜高在底面内的射影组成一个直角三角形;棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形正棱锥:如果一个棱锥的底面是正多边形,并且顶点在底面内的射影是底面的中心,这样的棱锥叫做正棱锥.棱锥的性质如果棱锥被平行于底面的平面所截,那么截面和底面相似,并且它们面积的比等于截得的棱锥的高和已知棱锥的高的平方比.